Maximum charge on the plates of a capacitor

[lorenz0]

Homework Statement

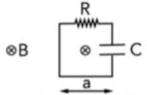
A square circuit of side $a=10cm$ with a resistance $R=1k\Omega$ and a capacitor $C=100nF$ is in a region of space where there is a $\vec{B}$ field perpendicular to circuit, pointing inward, which changes according to $\frac{dB}{dt}=-0.01 T/s$
Find the maximum charge on the plates of the capacitor and which plate is going to be positively charged and which one is going to be negatively charged.

Relevant Equations

$\oint_{\Gamma}\vec{E}\cdot d\vec{l}=-\frac{d\phi(\vec{B})}{dt}$

What I have done:

The electromotive force due to Faraday's Law is: $\mathcal{E}=-\frac{d\phi(\vec{B})}{dt}=\frac{d}{dt}(Ba^2)=a^2\frac{dB}{dt}=-10^{-4}V.$
In the circuit, going around the loop in a clockwise fashion:
$\oint_{\Gamma}\vec{E}\cdot d\vec{l}=-\frac{d\phi(\vec{B})}{dt}\Rightarrow iR+\frac{q}{C}=\mathcal{E}\Rightarrow \frac{dq}{dt}R+\frac{q}{C}=\mathcal{E}\Rightarrow \frac{dq}{dt}=-\frac{q-C\mathcal{E}}{RC}$
$\Rightarrow \int_{0}^{q}\frac{d\bar{q}}{\bar{q}-C\mathcal{E}}=-\int_{0}^{t}\frac{d\bar{t}}{RC}\Rightarrow [\ln(\bar{q}-C\mathcal{E})]_{0}^{q}=-\frac{t}{RC}\Rightarrow \ln\left(-\frac{q}{C\mathcal{E}}+1\right)=-\frac{t}{RC}\Rightarrow q(t)=C\mathcal{E}(1-e^{-\frac{t}{RC}})$ so $q_{max}=C\mathcal{E}=\left(100\cdot 10^{-9}\cdot (-10^{-4})\right) C=-10^{-11} C$.

Since the current goes around in a clockwise fashion, the upper plate should be charge positively and the bottom one negatively.

Now, I have a doubt: does it make sense that $q_{max}$ comes out negative?

Other than that, is my solution correct? Thanks

 

[Gordianus]

Remember: $\Phi=\int \vec B \cdot d\vec S$. How did you choose $d\vec S$? Check signs

 

[lorenz0]

Remember: $\Phi=\int \vec B \cdot d\vec S$. How did you choose $d\vec S$? Check signs

$\phi=\int_{S}\vec{B}\cdot d\vec{S}$ and since $\vec{B}$ is pointing inside the page and the area is oriented with the normal pointing away from the page this becomes $\int_{S}(-B)dS=-B\int_{S}dS=-Ba^2$ so $\mathcal{E}=-\frac{d}{dt}\phi=-\frac{d}{dt}(-Ba^2)=a^2\frac{dB}{dt}.$