Maximum electric field from a blob

[Rob2024]

Homework Statement

Purcell and Morin EM Exercise 1.49:

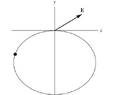
A point charge is placed somewhere on the curve shown in
Figure. This point charge creates an electric field at the origin.
Let $E_y$ be the vertical component of this field. What shape
(up to a scaling factor) should the curve take so that $E_y$ is inde-
pendent of the position of the point charge on the curve?
(b) You have a moldable material with uniform volume charge
density. What shape should the material take if you want to
create the largest possible electric field at a given point in
space? Be sure to explain your reasoning clearly.

Relevant Equations

Result for part a is the polar curve $r^2 = C \sin \theta$

For part a) we have $$ E = \frac{Qy}{4 \pi \epsilon_0 (x^2 + y^2)^{3/2} } = \text{constant} $$
I am stuck on part b). What should the shape of the volume?...

 

[haruspex]

Suppose you have chosen the direction for the resulting field at the target point. Consider the contributions from volume elements on the surface of the body. What can you say about them?

 

[Rob2024]

they need to be symmetric.

 

[haruspex]

they need to be symmetric.

Right, but consider changing the shape a bit by moving some of these surface elements around. If the shape is optimum, what will you find?

 

[Rob2024]

The problem I have with the argument of trying to use the first solution is that the first problem uses a fixed point charge. I am not too sure if we can turn a linear charge distribution into the point charge...i.e. I am not comfortable to say if we have a curve embedded in a uniformly charged volume will have the same amount of charge along the curve. In other words, maybe we could say find a curve with uniform charge density that yields the same y component electric field. This curve is not the same as the curve in the first solution.

 

[haruspex]

The problem I have with the argument of trying to use the first solution is that the first problem uses a fixed point charge.

No, it compares positions where a point charge may be placed. You need to do likewise in part b, as I hinted in post #4.
Please try to answer the question I posed there.

 

[Rob2024]

#5 has the answer to your question. I understand you are alluding to use the solution from part a) but I am not too sure if that's correct since part a)'s solution uses the condition $Q$ is constant. Thanks for the help. I'll think about this some more.

 

[haruspex]

#5 has the answer to your question.

It certainly does not have the answer I am looking for.
Given one shape for the body, you might try to increase the field by shifting little bits at the surface around (in a way that does not alter the direction of the field, by combining symmetric pairs of moves, say). If the shape is already optimum, what will you discover when trying this?