Maxwell Stress components of the energy-stress-momentum tensor

[milkism]

Homework Statement

Find the Maxwell Stress components

Relevant Equations

See solution.

Question:

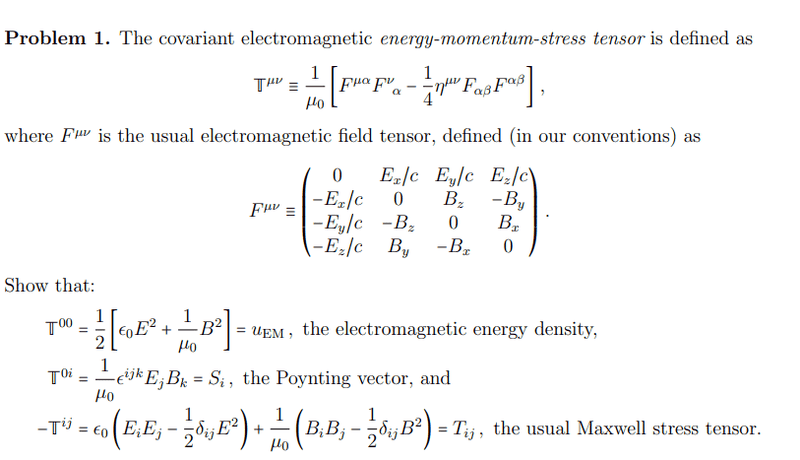
Solution:
I need help with the last part.

I think my numerical factors are incorrect, even if I add the last term it will get worse. What have I done wrong, or is there a better way to deal with this?

 

[TSny]

It's always a good idea to state the sign convention that you are using for the metric $\eta^{\mu \nu}$. I think you are using $\eta^{00} = -1$ and $\eta^{kk} = +1$.

We have $T^{\mu \nu} = \frac 1 {\mu_0} \left[ F^{\mu \alpha}F^{\nu}_{\,\,\, \alpha} - \frac 1 4 \eta^{\mu \nu} [ F_{\alpha \beta}F^{\alpha \beta}\right]$

Your calculation of the spatial components of the first part $T_f^{i j} = \frac 1 {\mu_0} F^{i \alpha}F^{j}_{\,\,\, \alpha}$ looks right except where you have

The $E_x^2$ in the first term in the brackets should be $E_z^2$. It's probably just a typo.

Then you write

I don't understand why you are adding together all of the $T^{i j}$. Instead, you should just be finding expressions for the individual $T^{i j}$, and also for $T^{0 0}$ and $T^{0 i}$.

 

[milkism]

Then you write
View attachment 326543
I don't understand why you are adding together all of the $T^{i j}$. Instead, you should just be finding expressions for the individual $T^{i j}$, and also for $T^{0 0}$ and $T^{0 i}$.

Do we need $T^{00}$ and $T^{0i}$? Because the latin indices go from 1 to 3. Or did I misunderstood the question.

 

[TSny]

Yes, latin indices go from 1 to 3.

The problem asks you to find expressions for $T^{0 0}, T^{0 i},$ and $-T^{i j}$.
So, you are essentially asked to find all the individual tensor components $T^{\mu \nu}$ for all values of the greek indices: $\mu, \nu = 0, 1, 2, 3$.

 

[milkism]

Yes, latin indices go from 1 to 3.

The problem asks you to find expressions for $T^{0 0}, T^{0 i},$ and $-T^{i j}$.
So, you are essentially asked to find all the individual tensor components $T^{\mu \nu}$ for all values of the greek indices: $\mu, \nu = 0, 1, 2, 3$.

I have already have done first and second, I just want to do third one.

 

[TSny]

I have already have done first and second, I just want to do third one.

Ok. So, you are now just interested in finding the $T^{i j}$ for $i, j = 1, 2, 3$. I see now where you stated that in the OP.

But I still don't understand why you are adding the various $T^{i j}$ together. That wouldn't have any physical meaning and the problem doesn't ask you to do that.

 

[milkism]

How else can I show that $-T^{ij}$ is equal to $\epsilon_0 \left( E_i E_j - \frac{1}{2} \delta_{ij} E^2 \right) + \frac{1}{\mu_0} \left( B_i B_j - \frac{1}{2} \delta_{ij} B^2 \right)$. Without finding out all terms, adding them all together, and simplifying it to the given formula.

 

[TSny]

There is no summation implied in the notation $T^{i j}$.

$T^{i j}$ represents any one of nine components $T^{11}, T^{12}, T^{13}, T^{21}, T^{22}, T^{23}, T^{31}, T^{32}, T^{33}$.

So, for example, you want to show that your result for $T^{12}$ agrees with the expression for $T^{i j}$ given below when $i = 1$ and $j = 2$.

 

[milkism]

Wow! I just wasted lots of time for nothing, well it's nothing compared to first exercise where I went by every single $\alpha$'s and $\beta$'s (16 terms), where you could have usen the known expression $F^{\alpha \beta} F_{\alpha \beta}$ for second part of the tensor.

 

[TSny]

Wow! I just wasted lots of time for nothing, well it's nothing compared to first exercise where I went by every single $\alpha$'s and $\beta$'s (16 terms), where you could have usen the known expression $F^{\alpha \beta} F_{\alpha \beta}$ for second part of the tensor.

I don't think you wasted your time in calculating the various $T^{i j}$.

I think there is a typographical error in the statement of the problem :

[EDIT] I believe it should read $$T^{0i} = \frac 1 {\mu_0 c} \epsilon^{ijk}E_jB_k = \frac{1}{c} S^i$$ if $\vec S$ is defined as usual: $\, \vec S = \frac 1 {\mu_0} \vec E \times \vec B \,\,\,$ (for free space).

 

[milkism]

I don't think you wasted your time in calculating the various $T^{i j}$.

I think there is a typographical error in the statement of the problem :
View attachment 326548
[EDIT] I believe it should read $$T^{0i} = \frac 1 c \epsilon^{ijk}E_jB_k = \frac{\mu_0}{c} S^i$$ if $\vec S$ is defined as usual: $\, \vec S = \frac 1 {\mu_0} \vec E \times \vec B \,\,\,$ (for free space).

Yes, that's true.

 

[milkism]

How can I show that $\partial _ \mu T^{\mu \nu} = 0$?
Or $\frac{\partial T^{0 \nu}}{c \partial t} + \frac{\partial T^{1 \nu}}{ \partial x^1} + \frac{\partial T^{2 \nu}}{ \partial x^2} + \frac{\partial T^{3 \nu}}{ \partial x^3} = 0$.

 

[TSny]

How can I show that $\partial _ \mu T^{\mu \nu} = 0$?
Or $\frac{\partial T^{0 \nu}}{c \partial t} + \frac{\partial T^{1 \nu}}{ \partial x^1} + \frac{\partial T^{2 \nu}}{ \partial x^2} + \frac{\partial T^{3 \nu}}{ \partial x^3} = 0$.

I guess you need to show this for free space where there is no charge density or current density (otherwise, the equation is not true).

Do you know how to express Maxwell's equations in terms of derivatives of $F^{\mu \nu}$?

If so, then you can show $\partial _ \mu T^{\mu \nu} = 0$ by first expressing $T^{\mu \nu}$ in terms of $F^{\alpha \beta}$ (as given at the beginning of Problem 1). Then try carrying out $\partial _ \mu T^{\mu \nu}$ and simplifying by using Maxwell's equations and the antisymmetry of $F^{\alpha \beta}$. There will be some index gymnastics involved.

 

[milkism]

I guess you need to show this for free space where there is no charge density or current density (otherwise, the equation is not true).

Do you know how to express Maxwell's equations in terms of derivatives of $F^{\mu \nu}$?

If so, then you can show $\partial _ \mu T^{\mu \nu} = 0$ by first expressing $T^{\mu \nu}$ in terms of $F^{\alpha \beta}$ (as given at the beginning of Problem 1). Then try carrying out $\partial _ \mu T^{\mu \nu}$ and simplifying by using Maxwell's equations and the antisymmetry of $F^{\alpha \beta}$. There will be some index gymnastics involved.

Wow, thought it would be easier.