- #1
Snazzy
- 470
- 0
[SOLVED]Mean of a probability distribution
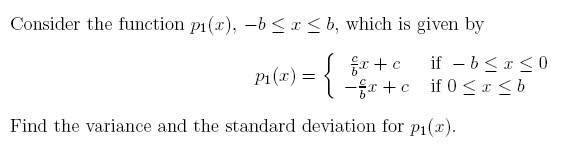
[tex]\int^{b}_{a}p(x)dx=1[/tex]
[tex]V=M_2-\bar{x}^2[/tex]
[tex]\bar{x}^2=\int^{b}_{a}xp(x)dx[/tex]
[tex]M_2=\int^{b}_{a} x^2p(x)dx[/tex]
I found that [tex]c=\frac{1}{b}[/tex] which is a right answer.
What I did next was:
[tex]
\bar{x}=\int^{b}_{-b}xp(x)dx[/tex]
[tex]=\int^{0}_{-b}x(\frac{cx}{b}+c)dx\ + \int^{b}_{0}x(\frac{-cx}{b}+c)dx[/tex]
[tex]= \int^{0}_{-b}\frac{cx^2}{b}\ +\ c\ dx\ + \int^{b}_{0}\frac{-cx^2}{b}\ +\ c\ dx[/tex]
[tex]=\left[ \frac{cx^3}{3b}+cx \right]_{-b}^{0}+\left[ \frac{-cx^3}{3b}+cx \right]_{0}^{b}[/tex]
[tex]=\frac{-2cb^3}{3b}+{2cb}[/tex]
[tex]=\frac{-2b^2}{3b}+\frac{2b}{b}[/tex]
[tex]=\frac{-2b}{3}+2
[/tex]
But the answer says that [tex]\bar{x}=0[/tex]
If I can manage to get x-bar, I can manage to get the variance and SD.
Homework Statement
Homework Equations
[tex]\int^{b}_{a}p(x)dx=1[/tex]
[tex]V=M_2-\bar{x}^2[/tex]
[tex]\bar{x}^2=\int^{b}_{a}xp(x)dx[/tex]
[tex]M_2=\int^{b}_{a} x^2p(x)dx[/tex]
The Attempt at a Solution
I found that [tex]c=\frac{1}{b}[/tex] which is a right answer.
What I did next was:
[tex]
\bar{x}=\int^{b}_{-b}xp(x)dx[/tex]
[tex]=\int^{0}_{-b}x(\frac{cx}{b}+c)dx\ + \int^{b}_{0}x(\frac{-cx}{b}+c)dx[/tex]
[tex]= \int^{0}_{-b}\frac{cx^2}{b}\ +\ c\ dx\ + \int^{b}_{0}\frac{-cx^2}{b}\ +\ c\ dx[/tex]
[tex]=\left[ \frac{cx^3}{3b}+cx \right]_{-b}^{0}+\left[ \frac{-cx^3}{3b}+cx \right]_{0}^{b}[/tex]
[tex]=\frac{-2cb^3}{3b}+{2cb}[/tex]
[tex]=\frac{-2b^2}{3b}+\frac{2b}{b}[/tex]
[tex]=\frac{-2b}{3}+2
[/tex]
But the answer says that [tex]\bar{x}=0[/tex]
If I can manage to get x-bar, I can manage to get the variance and SD.
Last edited: