Measurement and error (error estimation and propagation)

[otg]

Description of the situation
I have measured the incident number of electrons in a channel electron multiplier at different light polarization angles (a photoelectron angular distribution measurement). The events follow a poisson distribution and as far as I know the number of electron counts in a detector, C, has an error of $\sqrt{C}$.
I have used MATLAB cftool to make a fit to the measured data using a $\cos^2\theta$ function with a few parameters, giving me a value of one of the parameters as $$b=1.82\pm 0.12.$$
It looks kind of like this (not the actual data, but they are similar).

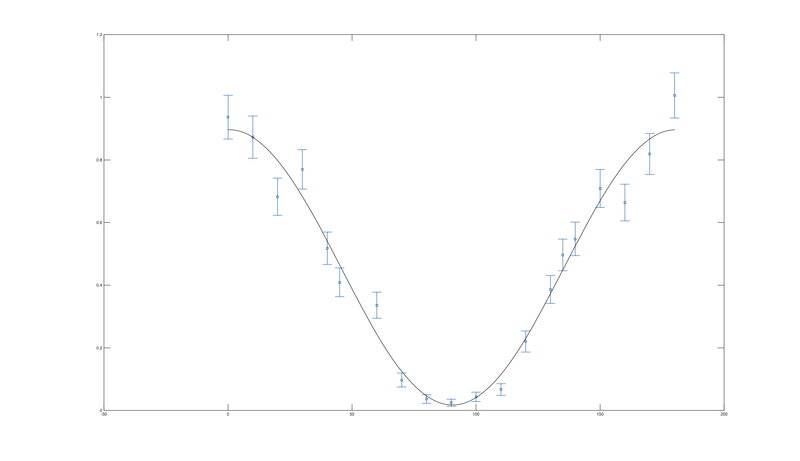
Another way to retrieve the value of $b$ is to use $C_0$ and $C_{90}$, hence the maximum and the minimum values of the angular distribution as seen in the attached picture. That is, the counts at $0^\circ$ and at $90^\circ$.

Problem
Assume that e.g. $C_0=900 \pm 30$ and $C_{90}=9 \pm 3$, and that I calculate the value $$\frac{C_0}{C_{90}}=q \pm \Delta q.$$ I then want to use $q$ to calculate $$b=\frac{1-q}{q+0.5}, $$ how do I find the full $b \pm \Delta b$ and $q \pm \Delta q$?

Attempt at a solution
Don't know if it's an attempt, but I calculated $q$ using all four combinations of $C_0 \pm \sqrt{C_0}$ and $C_{90} \pm \sqrt{C_{90}}$ (plus/minus, plus/plus, minus/plus and minus/minus). I then got four different $q$:s, and took the mean and calculated $\Delta q=|q_{mean}-\max(q_i)|$ for i=1:4 (or $\min(q_i)$, depending on what gave the largest error).
I then used the four combinations of $q$ to calculate four values of $b$ and retrieve the $\Delta b$ in the same manner.

The problem is that I now get $$b=1.82 \pm 0.012.$$ Perhaps not exactly, but the issue is that when I use two single data points my error is 10% of that I get using all data points and making a fit using the full function that (in theory) should correspond to the experiment.

My intuition tells me that the error in the last method should be at least as large, possibly larger, since it uses only two values and hence should be more sensitive to variations in the value $C$.

If anyone could help me out it would be of enormous help...

 

[mfb]

With your formulas and numbers, I get $q=100$ and $b\approx -1$. Something has to be wrong.

Your uncertainties on C₀ and C₉₀ are uncorrelated. You can evaluate the uncertainty for both separately and then add them in quadrature. It will probably become asymmetric as your relative uncertainty on C₉₀ is so large. Unfortunately that is not the correct asymmetry - because your estimate of $C_{90}=9\pm3$ is not correct. This is easier to see in more extreme cases: What if your count is 0? Does that mean your measurement has an uncertainty of 0?

If you know the expected photon count (from theory or whatever), then you have a sqrt(n) uncertainty on what you will actually see. But the opposite direction only works approximately for large counts. The number of photons you observe is exact - you saw 9 photons and not 8 or 10. To estimate the expectation value, you need the question "given a specific expectation value, how likely is it to see 9 photons?" Feldman and Cousins discussed this in detail in their paper. If you want a good estimate, you'll have to take this into account. If you just want a rough approximation how large the uncertainty is, just take up- and downvariation from the $\pm 3$ and make an average of them.

 

[otg]

With your formulas and numbers, I get $q=100$ and $b\approx -1$. Something has to be wrong.

Your uncertainties on C₀ and C₉₀ are uncorrelated. You can evaluate the uncertainty for both separately and then add them in quadrature. It will probably become asymmetric as your relative uncertainty on C₉₀ is so large. Unfortunately that is not the correct asymmetry - because your estimate of $C_{90}=9\pm3$ is not correct. This is easier to see in more extreme cases: What if your count is 0? Does that mean your measurement has an uncertainty of 0?

If you know the expected photon count (from theory or whatever), then you have a sqrt(n) uncertainty on what you will actually see. But the opposite direction only works approximately for large counts. The number of photons you observe is exact - you saw 9 photons and not 8 or 10. To estimate the expectation value, you need the question "given a specific expectation value, how likely is it to see 9 photons?" Feldman and Cousins discussed this in detail in their paper. If you want a good estimate, you'll have to take this into account. If you just want a rough approximation how large the uncertainty is, just take up- and downvariation from the $\pm 3$ and make an average of them.

Thank you mfb for the reply, I see that I wrote the formula for 1/q instead of q, so that would give you the value b=2 instead.
I'll have a look at the paper and see if I can get a grip of it. Of course the $\sqrt{n}$ only works that far, and that my uncertainty doesn't go to zero as my counts go down...

 

[f95toli]

My general advice for someone struggling how to do this kind of calculation is look in the GUM ( Guide to the Expression of Uncertainty in Measurement). It is quite well written, has some nice example and is -literally- the last word when it comes how to do this since it published by the BIPM and is what is used by e.g. most international standards

See
http://www.bipm.org/en/publications/guides/gum.html

Note that estimates of uncertainty is just that: estimates. You always have to make a number of assumptions and there are lots of cases where there isn't a single "correct" way of doing it.
The most general way of doing this -which would also work in this case- is to do Monte Carlo simulations; this way you can easily e.g. use different distributions for all parameters. At the very least if would give you a way of checking your answer.

 

[otg]

My general advice for someone struggling how to do this kind of calculation is look in the GUM ( Guide to the Expression of Uncertainty in Measurement). It is quite well written, has some nice example and is -literally- the last word when it comes how to do this since it published by the BIPM and is what is used by e.g. most international standards

See
http://www.bipm.org/en/publications/guides/gum.html

Note that estimates of uncertainty is just that: estimates. You always have to make a number of assumptions and there are lots of cases where there isn't a single "correct" way of doing it.
The most general way of doing this -which would also work in this case- is to do Monte Carlo simulations; this way you can easily e.g. use different distributions for all parameters. At the very least if would give you a way of checking your answer.

Thank you for your reply. I'll have a thorough look in the GUM document!