- #1
crick
- 43
- 4
Consider a scattering between two particles a and b that produces two particles c and d: d is stable, while c decays in two other different particles e and f.
The first interaction is by strong force (time of interaction ##t_1\sim 10^{-23}s##, which is also the time of generation of c and d), the second is weak (time of decay of c ##t_2\sim 10^{-8}##).
$$a+b\to_{strong} c+d\to_{weak} (e+f)+d$$
Suppose that the pourpose is to measure the times of interaction and decay ##t_1## and ##t_2## above stated using the cross section measurements.----------By "measuring the cross section" I mean measuring the rate of particle detection of ##e ##and##f## as a function of ##W=M_c##, the mass of the ##c## state, which looks something like:
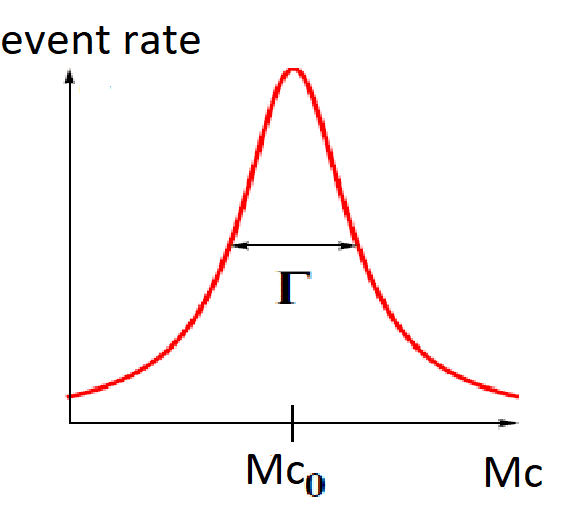
(For each value of ##M_c##, ##e## and ##f## will have to satisfy conditions on energy and momentum).
Now, are the following two considerations true?
- The time of weak decay of c is only linked to ##\Gamma## as $$t_2 \sim \hbar/\Gamma$$
- The time of interaction by strong force in the scattering of a and b (i.e. the time of generation of c state) is only linked to the integral of the curve above in a region around ##M_{c,0}##. Let's call this integral ##I## : then $$t_1 \sim 1/I$$
My reasoning is that, since c is generated by strong force in ##t_1##, this is the time that determines also the rate of production of ##e## and ##f##, which is the one I measure (c is not measurable in practice). But is this hypotesis correct?
The first interaction is by strong force (time of interaction ##t_1\sim 10^{-23}s##, which is also the time of generation of c and d), the second is weak (time of decay of c ##t_2\sim 10^{-8}##).
$$a+b\to_{strong} c+d\to_{weak} (e+f)+d$$
Suppose that the pourpose is to measure the times of interaction and decay ##t_1## and ##t_2## above stated using the cross section measurements.----------By "measuring the cross section" I mean measuring the rate of particle detection of ##e ##and##f## as a function of ##W=M_c##, the mass of the ##c## state, which looks something like:
(For each value of ##M_c##, ##e## and ##f## will have to satisfy conditions on energy and momentum).
Now, are the following two considerations true?
- The time of weak decay of c is only linked to ##\Gamma## as $$t_2 \sim \hbar/\Gamma$$
- The time of interaction by strong force in the scattering of a and b (i.e. the time of generation of c state) is only linked to the integral of the curve above in a region around ##M_{c,0}##. Let's call this integral ##I## : then $$t_1 \sim 1/I$$
My reasoning is that, since c is generated by strong force in ##t_1##, this is the time that determines also the rate of production of ##e## and ##f##, which is the one I measure (c is not measurable in practice). But is this hypotesis correct?
