- #1
Xynon
- 6
- 1
Consider that we have a magnet and a magnetometer (a fluxgate magnetometer with a single coil), standing still as shown in fig 1.
In fig 1, the magnetic field measured at the axis z1 of the magnetometer coil is B1.
But if everything (magnet, magnetometer and the axes) was rotating together around the x-axis as in fig 2, would there be a decrease in the measured magnetic field on the coil axis z1 due to the retarded angular position ∆θ? In other words, a tilt in the opposite direction of the rotation which decreases the component of B1 on the coil axis z1 ?
If so, could we state that B'1=B1 cos (∆θ) ?
Can we say that this angle of tilt ∆θ is a phase shift, if we consider the rotating magnet as a transmitting and the coil as a receiving antenna?

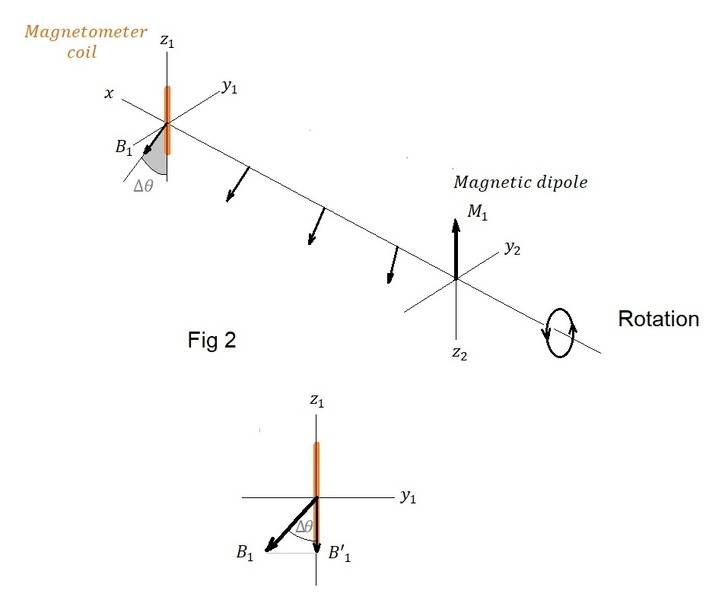
In fig 1, the magnetic field measured at the axis z1 of the magnetometer coil is B1.
But if everything (magnet, magnetometer and the axes) was rotating together around the x-axis as in fig 2, would there be a decrease in the measured magnetic field on the coil axis z1 due to the retarded angular position ∆θ? In other words, a tilt in the opposite direction of the rotation which decreases the component of B1 on the coil axis z1 ?
If so, could we state that B'1=B1 cos (∆θ) ?
Can we say that this angle of tilt ∆θ is a phase shift, if we consider the rotating magnet as a transmitting and the coil as a receiving antenna?

