Measuring wavelength of microwave radiation using double slits

[member 731016]

Homework Statement

Pls see below

Relevant Equations

Pls see below

For this problem,

The solution is,

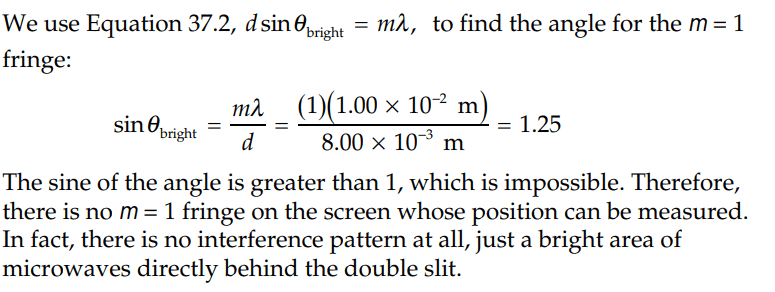
However, when they found the angle, they did not account for the uncertainty. I guess this is allowed still since the sine of the angle will still be greater than 1, correct?

Many thanks!

 

[kuruman]

However, when they found the angle, they did not account for the uncertainty. I guess this is allowed still since the sine of the angle will still be greater than 1, correct?

Would accounting for the uncertainty bring the value of the sine to less than 1? What do you think?

 

[member 731016]

Would accounting for the uncertainty bring the value of the sine to less than 1? What do you think?

Thank you for your reply @kuruman!

No it would not. Is that the justification they made for not accounting for the uncertainty?

Many thanks!

 

[kuruman]

No it would not. Is that the justification they made for not accounting for the uncertainty?

I don't know. I can't speak for them.

 

[member 731016]

I don't know. I can't speak for them.

Thank you for your reply @kuruman!

Oh, is that the justification you would make then?

Many thanks!

 

[kuruman]

Oh, is that the justification you would make then?

Nope. It would be the justification you provided in post #3.

 

[member 731016]

Nope. It would be the justification you provided in post #3.

Thank you for your help @kuruman!

Sorry, I meant to the justification in post #3.

Many thanks!

 

[Steve4Physics]

However, when they found the angle, they did not account for the uncertainty. I guess this is allowed still since the sine of the angle will still be greater than 1, correct?

A few additional thoughts…

Assume that the ±5% uncertainty determines the allowed range of $\lambda$. Then $\lambda$ must be between 0.95 cm and 1.05 cm.

(Though note that if ‘5%’ is a standard deviation, then $\lambda$ can be outside this range.)

The smallest possible value of $\sin \theta_{bright}$ (for m=1) is determined by the smallest possible value of $\lambda$. So, IMO, the model-answer calculation should have been done using $\lambda$ = 0.95 cm rather than $\lambda$ =1.00cm.

But really, no calculation is needed. It is not difficult to argue that the formation of any bright fringes is not physically possible if $\lambda \gt d$.

 

[member 731016]

A few additional thoughts…

Assume that the ±5% uncertainty determines the allowed range of $\lambda$. Then $\lambda$ must be between 0.95 cm and 1.05 cm.

(Though note that if ‘5%’ is a standard deviation, then $\lambda$ can be outside this range.)

The smallest possible value of $\sin \theta_{bright}$ (for m=1) is determined by the smallest possible value of $\lambda$. So, IMO, the model-answer calculation should have been done using $\lambda$ = 0.95 cm rather than $\lambda$ =1.00cm.

But really, no calculation is needed. It is not difficult to argue that the formation of any bright fringes is not physically possible if $\lambda \gt d$.

Thank you for your help @Steve4Physics!

Sorry I forgot about this thread.