Mechanical Principles -- Assignment question

[Al_Pa_Cone]

Can anyone help me? I have a question with 3 part answers on my Mechanical Principles assignment. I believe I have answered question part 'a' and 'b' but I have been stuck on question part 'c' for days!
So the question is:

Q5. The simply supported beam shown in FIG 4 is 5meters long with a Young’s Modulus of 210GN m-2 The cross section of the beam is as shown in FIG 5

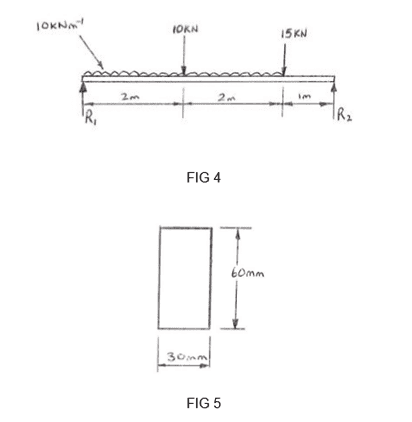.(a) Draw the shear force diagram for the beam
Solution:

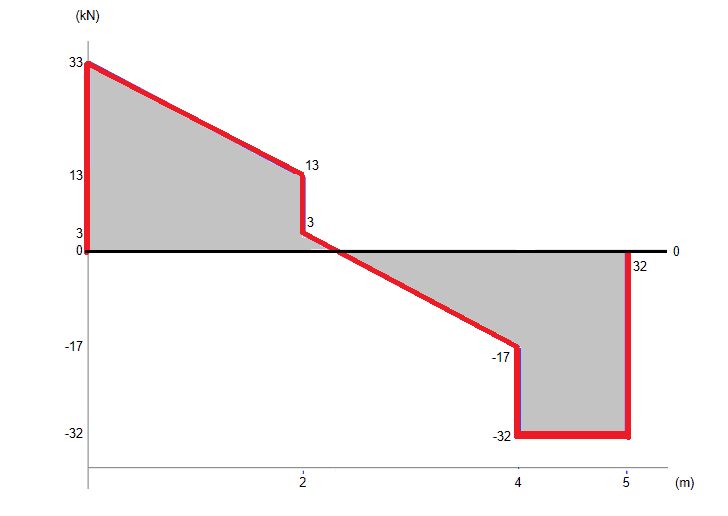
(b) Determine the position and magnitude of the maximum bending moment.
Solution:
Giving the moments at 1 meter intervals..

(c) Plot a graph of deflection along the length of the beam (calculate the deflection at 1m intervals).
Solution so far..

I understand as it has a U.D.L over a 4 meter spread we can focus the weight at its half way point,
4 * 10 kN = 40kN at 2m(half way) from R1.
As there already is a load at 2meters from R1 of 10 meters, This should increase the total load to 50 kN?

The Equations I believe are relevant to this are M/I = E/R where:
M= bending moment
I = The Second Moment of Inetria
E = The Youngs Modulus (210GN m-2)
R = Radius of curvature of the beam

M/EI = d2y/dx2

I = WL3/3EYmax

I think I need to work this out using Macauley's method, and it looks difficult. Can anyone advise on nice simple formula to use for each meter interval of deflection?

 

[haruspex]

Giving the moments at 1 meter intervals..

Is that adequate? The peak moment might be somewhere else.
For part c, if you have an equation for d²y/dx², valid over some range, how do you find the change in dy/dx over that range?

 

[Al_Pa_Cone]

Thats the question I have been set. adequate or not I am required to give the answer in 1 meter intervals. it looks like a long method of working out is required. I will spend some time on it this afternoon and see if I can get anywhere

 

[Al_Pa_Cone]

Ahh I see, You are suggesting my answer in part 'b' is not adequate? not the question set in part 'c' I apologise, Maybe I should go back and work out the bending moment at a smaller interval between 3 meters and 3.5 meters. That way I would have a more accurate answer.

 

[Al_Pa_Cone]

With that bit sorted, I am still stuck on question part C

 

[haruspex]

View attachment 110051
With that bit sorted, I am still stuck on question part C

You have the right answer to b now, but that is not the best way. For each interval (i.e. the span between two points where something in the loading changes suddenly) you should write an agebraic expression for how the moment varies across it. You can then differentiate them to find the peak moment in each interval. That way you do not have to guess how finely to cut it up.

That method becomes vital in answering part c. You did not try to answer my question. If you know the slope of a curve (dy/dx) at all points over some interval, how do you calculate the change in y across the interval?

 

[Al_Pa_Cone]

Thanks for you help so far, I was working on part 'c' yesterday but I didnt get round to posting my work so far. So here it is:

So I believe the equations above would provide me with the correct answers if I input all the known measurements into them?

I can only use the information I am provided in my current and previous lessons to figure out the answers to the set questions. Unless it is an oversite on my part, I am not aware of an equation given in these lessons, which would allow me to obtain the answer to question part 'b' in a different way. My process of elimination method was used in a previous assignment and I have just transferred the method to suit this situation. Could you advise of a better way of solving part 'b' as I have already demonstrated an understanding of the subject and provided a correct answer?

Thanks

 

[haruspex]

Thanks for you help so far, I was working on part 'c' yesterday but I didnt get round to posting my work so far. So here it is:View attachment 110100
So I believe the equations above would provide me with the correct answers if I input all the known measurements into them?

I can only use the information I am provided in my current and previous lessons to figure out the answers to the set questions. Unless it is an oversite on my part, I am not aware of an equation given in these lessons, which would allow me to obtain the answer to question part 'b' in a different way. My process of elimination method was used in a previous assignment and I have just transferred the method to suit this situation. Could you advise of a better way of solving part 'b' as I have already demonstrated an understanding of the subject and provided a correct answer?

Thanks

That's the right approach, but there are several things I do not understand in your working.
Where exactly is x measured from? Is your first equation only valid for a point in a specific interval?
Having x-a and x-b looks odd. I would have expected a + sign in one of them.
What about the distributed load? I don't see that in the equation.

 

[Al_Pa_Cone]

Ok, Today I have spend a lot of time going over and over Macaulays method and I believe I have come up with the answer which I can represent in the 1 meter intervals as required. Hopefully you will be able to see all the information in my working out for this to make sense?

So to continue this method I would simply substitute the value of x for 4,3,2 and 1 which should give me the results in 1 meter intervals as required?

Thanks

 

[haruspex]

Ok, Today I have spend a lot of time going over and over Macaulays method and I believe I have come up with the answer which I can represent in the 1 meter intervals as required. Hopefully you will be able to see all the information in my working out for this to make sense?
View attachment 110106 View attachment 110107
So to continue this method I would simply substitute the value of x for 4,3,2 and 1 which should give me the results in 1 meter intervals as required?

Thanks

That's a lot better, but you have not handled the distributed load correctly. See https://www.codecogs.com/library/engineering/materials/beams/macaulay-method.php.
Also, I trust you realize that when evaluating these expressions for some value of x, any term for which the bracket (x-a_i) is negative should be ignored.

 

[Al_Pa_Cone]

Thanks for all your help on this one. I will get round to re-calculating my answer at some point today. Its hard juggling a full time job and looking after my 1year old whilst taking on a HNC!

I will post my workings later on today hopefully.

 

[Al_Pa_Cone]

Does this look like the correct method to follow, pre- integration of course?

or would it be the better to deal with each as a separate equation and subtract the results at the end?

 

[haruspex]

View attachment 110307
Does this look like the correct method to follow, pre- integration of course?

or would it be the better to deal with each as a separate equation and subtract the results at the end?

Yes, that all looks right. I would not have put the R₁ term in the distributed component, but you avoided writing 2R₁ when you combined them, so that's ok.

 

[Al_Pa_Cone]

Can you expand on your comment, "I would not have put the R_1 term in the distributed component"?
Is it the way I have expressed the value in an algebraic form 'R_1' as simply 'R' would surfice or do I need to change my calculation method in a way which does not include the 33 kN which the R_1 term is representing?

 

[haruspex]

Can you expand on your comment, "I would not have put the R_1 term in the distributed component"?
Is it the way I have expressed the value in an algebraic form 'R_1' as simply 'R' would surfice or do I need to change my calculation method in a way which does not include the 33 kN which the R_1 term is representing?

Perhaps I misunderstood your approach. I guess you treated it as two different problems, one with point loads and one with a distributed load, but each having an end support. So when you merged them you still had just the one instance of R.
Previously I read it as one equation that included all point forces (including end support) and one for all distributed (which would not include R), then directly adding them.

Same result.

 

[Al_Pa_Cone]

So the equation solution above would be the correct method to follow?

When I collect all the results I will post them and plot a graph as required

 

[haruspex]

So the equation solution above would be the correct method to follow?

When I collect all the results I will post them and plot a graph as required

Yes, it should work. Just bear in mind what I wrote at the end of post #10

 

[Al_Pa_Cone]

I have come up against another problem. In post 13 I gave an equation to deal with the UDL load and algibraically expressed the value of (x-a) and (x-b).

Then combining the two equations with the method for dealing with a point load, which also contains an algebraic expression of (x-a) and (x-b). However, as x = distance between 0 and 5 suits both equations, the relevancy of a and b in the U.D.L equation become unclear.

Are these values (a and b) in the UDL equation the start and finish point of the UDL, so 0-4. As they represent the distance from R to the first and second point load in the second equation therefore should be expressed as a different algebraic term. Maybe c and d for example?

 

[haruspex]

Are these values (a and b) in the UDL equation the start and finish point of the UDL, so 0-4. As they represent the distance from R to the first and second point load in the second equation therefore should be expressed as a different algebraic term. Maybe c and d for example?

Yes, sorry, I omitted to check you had the bounds right for the UDL. The two constants in the UDL terms should be the offsets from 0 (left hand end) to the start and end points of the UDL. So, 0 and 4, not 2 and 4.

 

[Al_Pa_Cone]

ok for my full revised workings including integration of the two combined formula, Whats do you think to my solution?

 

[haruspex]

ok for my full revised workings including integration of the two combined formula, Whats do you think to my solution?
View attachment 110461 View attachment 110462

Nearly right. Check those '9' denominators.

 

[Al_Pa_Cone]

Would I be right in thinking the denominator should be 12? As the UDL equation begins integration with a denominator of 2 and then multiplied by 2 becomes 4, then multiplied by 3 becomes 12?

 

[haruspex]

Would I be right in thinking the denominator should be 12? As the UDL equation begins integration with a denominator of 2 and then multiplied by 2 becomes 4, then multiplied by 3 becomes 12?

Yes.

 

[Al_Pa_Cone]

Ok Thanks for all your help, I really appreciate it!
I have done all my working out and discounted any negative values in the brackets as required. I will now post all my working out and finally the results I have obtained into a graph, Does this look correct?

As this involves so much effort to obtain a correct answer, I am hoping this is good enough? I have spent over 3 weeks on this one question!

 

[haruspex]

Ok Thanks for all your help, I really appreciate it!
I have done all my working out and discounted any negative values in the brackets as required. I will now post all my working out and finally the results I have obtained into a graph, Does this look correct?

View attachment 110552
View attachment 110553
View attachment 110554
View attachment 110556 View attachment 110557 View attachment 110558
View attachment 110559

As this involves so much effort to obtain a correct answer, I am hoping this is good enough? I have spent over 3 weeks on this one question!

You seem to have omitted the Ax term. A should be such that it gets back to zero deformation at the 5m mark. (I get -149/6 for A.)
I don't understand your B= statements. B is a constant, and it must be zero so that deformation is zero at x=0. The value to be calculated at each x is the y value.
The full graph should be quite smooth. I just put your formula into Google sheets and it looks convincing.

 

[Al_Pa_Cone]

I just followed my method of obtaining the value of A to obtain a value for B. I read an example where be was equal to zero when x was equal to 5 but I couldn't figure out whether it was only relevant to the example or applied to my answers, and if so when does be become something other than zero, and how should I go baout obtaining B?

 

[haruspex]

I just followed my method of obtaining the value of A to obtain a value for B. I read an example where be was equal to zero when x was equal to 5 but I couldn't figure out whether it was only relevant to the example or applied to my answers, and if so when does be become something other than zero, and how should I go baout obtaining B?

Let's go back to your equation in post #20, but with 12s instead of 9s in the denominators.
You have $y=\Sigma c_i(x-d_i)^{n_i} + Ax+B$, where it is understood that in evaluating y(x) we ignore any terms with d_i>x.
The next step is to determine A and B. These are fixed by the knowledge that y(0)=y(5)=0.
Obviously y(0)=B, so B=0. Evaluate y(5) to find A. Then you are ready to find y at intermediate points.

In your post #24 you have not applied Macaulay's rule correctly. You discarded the -27 term, but you should have discarded the next two as well. (1-2)² is positive, but that is not what matters. The 1-2 is negative, so the term should be discarded.

 

[haruspex]

I just put your formula into Google sheets and it looks convincing.

Hmm.. actually it looks wrong... investigating...

OK, found it. There is another error I missed before. When you integrated the spread load terms you divided by 3 but lost an existing 1/2 factor. So in the displacement equation those two denominators should be 24, not 12. With those corrections I at last get a reasonable graph - see next post.

 

[haruspex]

 

[Al_Pa_Cone]

This is all very confusing. So my post #22 where I calculated the denominatiors through the integration process was incorrect and the final state of the two UDL denominators should have been 24 not 12, Once I have gained that information I can work back through your post on #27 and hopefully obtain a graph much like yours.

Thanks

 

[haruspex]

post #22 where I calculated the denominatiors through the integration process was incorrect

It was already wrong in post #20. In the $\frac {d^2}{dy^2}$ equation you had, correctly, a term $-\frac{(10)(x-0)^2}{2}$. But when you integrated that you got $-\frac{(10)(x-0)^3}{3}$ instead of $-\frac{(10)(x-0)^3}{6}$. Same with the next term.

 

[Al_Pa_Cone]

This is my working out for A when x = 5, and B = 0,

I am completely lost as to how I obtain the value for A when B does not equal 0, I would think A is worth a different value as x changes?
I presume I am plotting onto the graph for the value of B anyway?

Do I need to use the math methods for finding 2 unknowns or is their a much simpler way. Obvioiusly Understanding Calculus is not my strong point in all of this!

Thanks

 

[haruspex]

am completely lost as to how I obtain the value for A when B does not equal 0

A and B are constants, by definition. You correctly found that B must be zero in order that y(0)=0, then you found that A=-76 so that y(5)=0.
There is no more to do, you have the complete equation. Just sketch the curve and see if you get something like the graph I posted.

 

[Al_Pa_Cone]

but what about the deflection values for 2,3and 4 meters as the question requires me to give results in 1 meter increments. Also how would I find out to what level the curve should drop to before it begins to climb back to 0? I would have thought they expect me to plot each point and then build a curve from the known results.

 

[haruspex]

but what about the deflection values for 2,3and 4 meters

Just plug those x values into the equation.
You seem not to understand the statement that A and B are constants. Having determined what they are by considering particular (x,y) pairs, they apply for all x.
Think of it this way. Without knowing A and B, you have an equation which satisfies all the loads, but works no matter how high the two supports are. You can adjust each up and down independently, and the beam displacements will adjust to match. That is equivalent to varying A and B. In the actual set-up, y is defined to be 0 at the left support, and the right hand support is at the same height. A and B must have those values which give y(0)=y(5)=0.

how would I find out to what level the curve should drop to before it begins to climb back to 0

I don't see that asked for in the question as you posted it. If you have to find that, the ideal method would be to find where the gradient is zero. But the gradient equation contains cubic terms, so you would have to solve a cubic equation, which I am sure you are not expected to do. Next best is to plot the curve using some software and read it off the graph. Third best is to calculate y at a number of points; the more the merrier, but the question as you posted it specifies 1m intervals... a bit crude, but that's what it says.