guyvsdcsniper
- 264
- 37
- Homework Statement
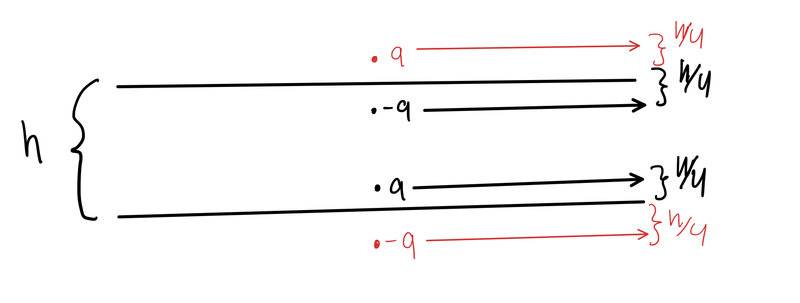
- Find the force on p.c. q placed inside a parallel plate capacitor in
vacuum, with grounded plates, separated at distance h. The point charges are at
distance h/4 from the closest plate
- Relevant Equations
- F=qe
Before I can find the force on q I must balance the charges. This problem starts of with -q and q inside the capacitor. I have added image charges on the opposite side of each plate. Would this work?