Methods to compute bounds on polynomial roots (not close yet)

In summary, The polynomial given is a Hurwitz polynomial and the bounds for its roots can be found using various methods such as Rouche, Lagrange, Cauchy, and Fujiwara. However, these bounds may not be accurate and additional methods such as McLaurin's and Newton's inequalities can be used to refine them. The precise annulus containing all the zeros of the polynomial can also be determined using a contour integral and the argument principle with a binary search approach.
  • #1
aheight
321
109
TL;DR Summary
Reviewing methods to compute bound on roots to polynomials. The bounds are quite large and wanted to know if there are any better.
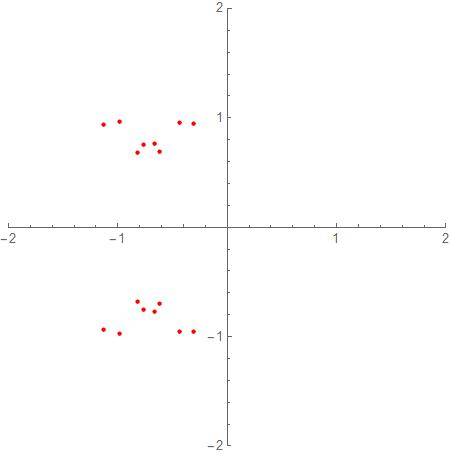
Consider an example polynomial:
$$
\begin{align*}
P_{16}(z)&=0.0687195 z^{16}+0.787411 z^{15}+4.58749 z^{14}+17.7271 z^{13}+50.5007 z^{12}\\
&+111.995 z^{11}+199.566 z^{10}+291.128 z^9+351.292 z^8+351.927 z^7+292.066 z^6\\
&+199.046 z^5+109.514 z^4+47.2156 z^3+15.1401 z^2+3.25759 z+0.362677
\end{align*}
$$
and a plot of the roots in the complex plane below. They are bounded by a circle of radius 2. The following disc size for the bounds is what I get using four calculations in the Wikipedia article dealing with root bounds found here: Bounds for polynomial roots :

Rouche: 17
Lagrange: 29774
Cauchy: 5122
Fujiwara: 22

These seem to be a very poor estimate of the bounds. I was wondering if anyone knew methods to narrow the bound down?

rootPlot.jpg
 
  • Like
Likes BvU
Mathematics news on Phys.org
  • #2
A first glimpse on the French version of your link looks as if there were some additional formulas. If you cannot read French, then use Chrome and its translation function. I think this is a better list:
https://en.wikipedia.org/wiki/List_of_numerical_analysis_topics#Finding_roots_of_nonlinear_equations

Another observation from the above is, that your polynomial is a Hurwitz polynomial (the English version on Wikipedia is poor, French and German are better in this case). You could search the internet for more information on it. Further hints on how to get better algorithms might be McLaurin's and/or Newton's inequalities.
 
  • Like
Likes aheight
  • #3
I've been looking at other methods. Apparently there are many. See: Inequalities for polynomials. Many seem to be bounded by ##a_n## in the denominator which in my case ##a_n=0.068## and being very small, causes bound to be large. However in the reference above, Theorem 17 gives this bound:

If:
##P(z)=a_0+a_1 z+\cdots+a_n z^n##

then let:

##\displaystyle B(w)=\frac{1}{a_0 w^n+\cdots+a_n}##

Then an upper bound (R) on the zeros is given by:

##
R\leq e \overline{\lim}_{k\to\infty}\frac{\sqrt[k]{|B^{(k)}(0)|}}{k}
##

but it doesn't say what ##B^{(k)}## is. I think it's k'th derivative but not sure. Would anyone know?
 
  • #4
The exact answer to your question costs $38. I guess it is safe to assume it is the k-th derivative.
 
  • #5
fresh_42 said:
The exact answer to your question costs $38. I guess it is safe to assume it is the k-th derivative.
Yes, I tried searching " The precise annulus containing all the zeros of a polynomial " and it's behind all kinds of pay walls and cookies. Usually though an appeal directly to the author gets results I've found. But I can run it through Mathematica using the derivative; can do amazing number crunching with Mathematica. :)
 
  • Like
Likes fresh_42
  • #6
Thought I'd post my results: I ran the expression with 40 derivatives and obtained the plot below.

Updated (forgot the E term in the limit): Looks like the limsup is tending towards around 5 which is not bad. It took 1 minute at 4.5 GHz to run.
rootPlot.jpg
 
Last edited:
  • Like
Likes fresh_42
  • #7
You could use one of the bounds mentioned on Wikipedia as a crude but easy-to-compute upper bound, and then use the argument principle to refine this bound with a binary search. E.g. since the Rouche bound of your original polynomial was ##17##, compute the contour integral ##\frac{1}{2i\pi}\oint_{\gamma(r)}\frac{P’(z)}{P(z)}dz## where ##\gamma(r)## is a circle of radius ##r##. Let ##r## start at ##17## and perform contour integrations at ##17##, ##8.5##, ##4.25##, ##2.125##, ##1.0625##, ##\frac{2.125+1.0625}{2}## ... etc. At ##r=1.0625## the integral will drop below ##16##, showing that there are less than ##16## roots inside the circle.
 
  • Like
Likes aheight
  • #8
suremarc said:
You could use one of the bounds mentioned on Wikipedia as a crude but easy-to-compute upper bound, and then use the argument principle to refine this bound with a binary search. E.g. since the Rouche bound of your original polynomial was ##17##, compute the contour integral ##\frac{1}{2i\pi}\oint_{\gamma(r)}\frac{P’(z)}{P(z)}dz## where ##\gamma(r)## is a circle of radius ##r##. Let ##r## start at ##17## and perform contour integrations at ##17##, ##8.5##, ##4.25##, ##2.125##, ##1.0625##, ##\frac{2.125+1.0625}{2}## ... etc. At ##r=1.0625## the integral will drop below ##16##, showing that there are less than ##16## roots inside the circle.
I think the real difficulty is to determine the center of ##\gamma(r)##, and to consider only the relevant half of all complex roots. Considering all roots and the origin as center probably led to the less efficient bounds.
 
  • #9
fresh_42 said:
I think the real difficulty is to determine the center of ##\gamma(r)##, and to consider only the relevant half of all complex roots. Considering all roots and the origin as center probably led to the less efficient bounds.
Why should the center be anything besides 0? Here we are considering the magnitude of the largest root, ie the largest disk centered at 0 containing all of the roots.

If we’re talking about the diameter of the set of roots, I think that is different from what OP is asking.
 
  • #10
suremarc said:
You could use one of the bounds mentioned on Wikipedia as a crude but easy-to-compute upper bound, and then use the argument principle
Very nice! Here's the complete code to compute (confirm) Rouche's bound of 17, then three binary searches using arg principal, and the resulting boundary circles zeroing in on the outermost zero. Note the plot of zeros is different than first plot because I am only using 6 digits of precision in the definition of the function for brevity of code.

Mathematica: 
(*
 get roots
*)
zFun[z_] =
  0.362677 + 3.25759 z + 15.1401 z^2 + 47.2156 z^3 + 109.514 z^4 +
   199.046 z^5 + 292.066 z^6 + 351.927 z^7 + 351.292 z^8 +
   291.128 z^9 + 199.566 z^10 + 111.995 z^11 + 50.5007 z^12 +
   17.7271 z^13 + 4.58749 z^14 + 0.787411 z^15 + 0.0687195 z^16;
theRoots = Sort[z /. NSolve[zFun[z] == 0, z]]
(*
 Rouche's bound:  confirm r=17 is the bound as per theorem
*)
cList = CoefficientList[zFun[z], z]
rVal = 17
max1 = Last@cList rVal^16
max2 = Sum[Abs[cList[[n]] ] rVal^(n - 1), {n, 1, Length@cList - 1}]
max1 > max2
(*
 get first bound from Rouche's estimate
*)
theR = 17;
currentVal = 100;
While[Re@currentVal >= 15.5,
  theR = theR/2;
  currentVal =
   1/(2 Pi I) NIntegrate[(D[zFun[z], z]/zFun[z] (I theR Exp[I t])) /.
      z -> theR Exp[I t], {t, -Pi, Pi}];
  ];
r1 = theR;
rOuter = 2 theR;
rInner = theR;
(*
 now have annulus of rOuter and rInner.  Second binary search in \
annuli:
*)
currentR = rOuter;
deltaR = (rOuter - rInner)/10;
currentVal = 100;
While[Re@currentVal >= 15.5,
  currentR -= deltaR;
 
  currentVal =
   1/(2 Pi I) NIntegrate[(D[zFun[z], z]/
        zFun[z] (I currentR Exp[I t])) /.
      z -> currentR Exp[I t], {t, -Pi, Pi}];
  ];
(*
 third search
*)
r2 = currentR;
rOuter = currentR + deltaR;
rInner = currentR;
currentR = rOuter;
deltaR = (rOuter - rInner)/10;
currentVal = 100;
While[Re@currentVal >= 15.5,
  currentR -= deltaR;
  currentVal =
   1/(2 Pi I) NIntegrate[(D[zFun[z], z]/
        zFun[z] (I currentR Exp[I t])) /.
      z -> currentR Exp[I t], {t, -Pi, Pi}];
  ];
r3 = currentR;
(*
 plot results
*)
zRootsG =
  Graphics@{PointSize[0.0105], Red, Point@(ReIm@# & /@ theRoots)};
circle1 = Graphics@{Black, Circle[{0, 0}, r1]};
circle2 = Graphics@{Blue, Circle[{0, 0}, r2]};
circle3 = Graphics@{Red, Circle[{0, 0}, r3]};
plotA = Show[{zRootsG, circle1, circle2, circle3}, Axes -> True,
  PlotRange -> 2]

argBoundPlot.jpg
 
  • Like
Likes suremarc
  • #11
aheight said:
Yes, I tried searching " The precise annulus containing all the zeros of a polynomial " and it's behind all kinds of pay walls and cookies. Usually though an appeal directly to the author gets results I've found. But I can run it through Mathematica using the derivative; can do amazing number crunching with Mathematica. :)
You may find this paper of interest: https://arxiv.org/pdf/1312.0135.pdf. He computes the inner and outer radii in terms of binomial coefficients and Fibonacci numbers.
 
  • Like
Likes aheight
  • #12
Fred Wright said:
You may find this paper of interest: https://arxiv.org/pdf/1312.0135.pdf. He computes the inner and outer radii in terms of binomial coefficients and Fibonacci numbers.
In Theorem B of that paper, he gives a root boundary by the expression:
##r_2=2/3 \max\limits_{1 \leq k \leq n}\biggr\{\frac{F_{4n}}{2^n F_k\binom{n}{k}}\bigg|\frac{a_{n-k}}{a_n}\bigg|\biggr\}^{1/k}##

where ##F_k## is the Fibonacci number but ##F_{64}=10610209857723## and the other terms are relatively small giving me ##r_2## at about ##10^7## which is a poor estimate for at least this function. I could have made a mistake coding it but have checked it several times.

Mathematica: 
degree = 16;
cList = CoefficientList[zFun[z], z] // N;

cLen = Length@cList
myTable =
  Table[2/3 (Fibonacci[4 degree]/(
       2^degree Fibonacci[k] Binomial[degree, k])
        Abs[cList[[cLen - k]]/cList[[cLen]]])^(1/k), {k, 1, degree}];
Max@myTable
7.72955*10^7
 
  • #13
aheight said:
In Theorem B of that paper, he gives a root boundary by the expression:
##r_2=2/3 \max\limits_{1 \leq k \leq n}\biggr\{\frac{F_{4n}}{2^n F_k\binom{n}{k}}\bigg|\frac{a_{n-k}}{a_n}\bigg|\biggr\}^{1/k}##

where ##F_k## is the Fibonacci number but ##F_{64}=10610209857723## and the other terms are relatively small giving me ##r_2## at about ##10^7## which is a poor estimate for at least this function. I could have made a mistake coding it but have checked it several times.

Mathematica: 
degree = 16;
cList = CoefficientList[zFun[z], z] // N;

cLen = Length@cList

Max@myTable
7.72955*10^7
Disappointing to say the least. Did you express your polynomial in terms of Theorem A?
$$
Q(x) = x^n− |a_{n−1}|x^{n−1}− |a_{n−2}|x^{n−2}− · ·· − |a_1|x− |a_0|
$$
If so, I guess there is a limit on the order of the polynomial hiding behind the paywall at
J. L. D´ıaz-Barrero, An annulus for the zeros of polynomials, J. Math. Anal. Appl., 273 (2002)
349-352. This must be a case of "you get what you pay for".:H Sorry to waste your time.
 
  • #14
Fred Wright said:
Disappointing to say the least. Did you express your polynomial in terms of Theorem A?
$$
Q(x) = x^n− |a_{n−1}|x^{n−1}− |a_{n−2}|x^{n−2}− · ·· − |a_1|x− |a_0|
$$
If so, I guess there is a limit on the order of the polynomial hiding behind the paywall at
J. L. D´ıaz-Barrero, An annulus for the zeros of polynomials, J. Math. Anal. Appl., 273 (2002)
349-352. This must be a case of "you get what you pay for".:H Sorry to waste your time.

Never a waste of time: often the road to the solution is littered on both sides with wrong ones and the only way to get to the right one is to wade through the wrong ones. :)

Also I used the format specifically given in the theorem so I think that part is correct.
 

FAQ: Methods to compute bounds on polynomial roots (not close yet)

1. What are polynomial roots?

Polynomial roots are the values of the variable that make the polynomial equation equal to zero. For example, in the equation x^2 + 2x + 1 = 0, the roots are -1 and -1 because (-1)^2 + 2(-1) + 1 = 0.

2. Why is it important to compute bounds on polynomial roots?

Computing bounds on polynomial roots can help us determine the possible range of values for the roots. This can be useful in many applications such as optimization problems, signal processing, and data analysis.

3. What are some methods to compute bounds on polynomial roots?

Some common methods include the Rational Root Theorem, Descartes' Rule of Signs, and the Intermediate Value Theorem. Other methods include using the properties of complex numbers and using numerical methods such as bisection or Newton's method.

4. How accurate are the bounds obtained from these methods?

The accuracy of the bounds depends on the method used and the complexity of the polynomial. In general, the bounds obtained from these methods are not exact but provide a range within which the roots are guaranteed to lie.

5. Can these methods be applied to all types of polynomials?

Yes, these methods can be applied to all types of polynomials, including both real and complex polynomials. However, the complexity of the polynomial may affect the accuracy of the bounds obtained.

Hot Threads

Recent Insights

Back
Top