- #1
Petrus
- 702
- 0
Hello MHB,
Calculate \(\displaystyle A^{17}\) where
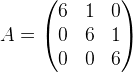 .
.
Progress,
I have multiplicate without adding them together to see a pattern and I can se at \(\displaystyle A^{17}\) on that matrice where it's 6's it will be \(\displaystyle 6^{17}\) and rest I can't se any pattern those riight side of the triangle, cause the left will be zero
Regards,
Calculate \(\displaystyle A^{17}\) where
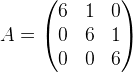
Progress,
I have multiplicate without adding them together to see a pattern and I can se at \(\displaystyle A^{17}\) on that matrice where it's 6's it will be \(\displaystyle 6^{17}\) and rest I can't se any pattern those riight side of the triangle, cause the left will be zero
Regards,