- #1
epsilon
- 29
- 1
I have been trying for hours to understand what is physically causing the interferometric rings to contract when the separation of the mirrors is reduced.
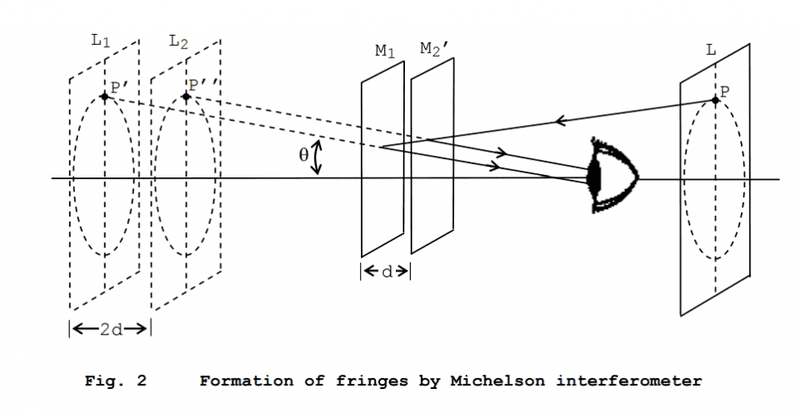
From the equation: [itex]m\lambda = 2Lcos\theta[/itex], where [itex]m[/itex] is the number of fringes, if we consider just one fringe at a fixed wavelength, [itex]m\lambda[/itex] is constant and hence [itex]2Lcos\theta[/itex] is also constant.
Hence reducing [itex]L[/itex] causes [itex]cos\theta[/itex] to increase, which is analogous to reducing [itex]\theta[/itex]. [Is this where I'm going wrong?]
Question 1: When reducing d in the image above, does it matter if we are moving [itex]L_1[/itex] towards [itex]L_2[/itex] or vice versa? (Is it directionally dependent?)
Question 2: The image suggests that [itex]\theta[/itex] is only linked to [itex]L_1[/itex]. If I move [itex]L_1[/itex] towards [itex]L_2[/itex], the adjacent side of the right-angled triangle is getting shorter, and hence [itex]\theta[/itex] must be increasing. But this goes against what happens when it is considered mathematically.
How can we tell PHYSICALLY whether the rings are contracting or expanding? Thank you.
From the equation: [itex]m\lambda = 2Lcos\theta[/itex], where [itex]m[/itex] is the number of fringes, if we consider just one fringe at a fixed wavelength, [itex]m\lambda[/itex] is constant and hence [itex]2Lcos\theta[/itex] is also constant.
Hence reducing [itex]L[/itex] causes [itex]cos\theta[/itex] to increase, which is analogous to reducing [itex]\theta[/itex]. [Is this where I'm going wrong?]
Question 1: When reducing d in the image above, does it matter if we are moving [itex]L_1[/itex] towards [itex]L_2[/itex] or vice versa? (Is it directionally dependent?)
Question 2: The image suggests that [itex]\theta[/itex] is only linked to [itex]L_1[/itex]. If I move [itex]L_1[/itex] towards [itex]L_2[/itex], the adjacent side of the right-angled triangle is getting shorter, and hence [itex]\theta[/itex] must be increasing. But this goes against what happens when it is considered mathematically.
How can we tell PHYSICALLY whether the rings are contracting or expanding? Thank you.