Minimal rotational kinetic energy for a gyroscope to precess

[Malwina]

TL;DR Summary: I cannot find any information on how to calculate min. KErot at which the gyroscope does not fall over

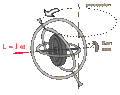
I am doing a project for school in which I investigate energy loss in a gyroscope. I apply a torque on a gyroscope to initiate its rotation and then measure the time it takes for the gyroscope to fall (its spinning axis is then at 45deg to the surface).

Now I'm trying to measure what is the kinetic energy lost due to surface friction and I have searched everywhere I could but I cannot seem to get a definite answer to my question: How do I calculate the smallest possible rotational kinetic energy at which my gyroscope will still precess, not fall?

I know it must be related to angular velocity but I did not find any specific formulas that would help me calculate it. I think I can calculate the work done by friction by multiplying the force of the gyroscope on the ground by the coefficient of static friction of my surface and by the distance the tip covers before falling.

Can someone help me out and provide any further sources on how to calculate the minimal energy the gyroscope needs to keep precessing and not falling?

 

[berkeman]

Welcome to PF.

Now I'm trying to measure what is the kinetic energy lost due to surface friction

If you mean the kinetic energy of the spinning gyroscope, that is only lost due to bearing friction in the gyroscope, no? I don't think it has much to do with the friction between the bottom support of the gyroscope and the table...

 

[jbriggs444]

How do I calculate the smallest possible rotational kinetic energy at which my gyroscope will still precess, not fall?

If you are looking for a sharp dividing line between a precessing rotation and a rotating fall, I do not believe that there is one.

This article on nutation shows at least some of the complexity lurking here.

 

[Malwina]

Welcome to PF.If you mean the kinetic energy of the spinning gyroscope, that is only lost due to bearing friction in the gyroscope, no? I don't think it has much to do with the friction between the bottom support of the gyroscope and the table...

Oh, thanks. I measured the time it took for the gyroscope to fall over on different types of surface (wood, glass, carpet) and I noticed that the bigger the coefficient of dynamic friction, the faster the gyroscope falls over (and it's a difference of 10-15 seconds on average, so I thought it was significant). If energy is not lost to friction then what can affect the different amount of time after which the gyroscope falls over?

 

[berkeman]

Oh, thanks. I measured the time it took for the gyroscope to fall over on different types of surface (wood, glass, carpet) and I noticed that the bigger the coefficient of dynamic friction, the faster the gyroscope falls over (and it's a difference of 10-15 seconds on average, so I thought it was significant). If energy is not lost to friction then what can affect the different amount of time after which the gyroscope falls over?

What kind of gyroscope are you using? If it is a simple gyroscope that has no low-friction bearings and no rigid support structure to the base, then the whole structure could be rotating which would give you additional friction losses dependent on the surface material.

https://www.collinsdictionary.com/us/dictionary/english/gyroscope

 

[Malwina]

What kind of gyroscope are you using? If it is a simple gyroscope that has no low-friction bearings and no rigid support structure to the base, then the whole structure could be rotating which would give you additional friction losses dependent on the surface material.

View attachment 338781
https://www.collinsdictionary.com/us/dictionary/english/gyroscope

Yes, I am using this gyroscope and I am putting the end shown on the second photo directly on the surface with no support structure. I think I can calculate the distance it covers by calculating the precession of the top, because they move the same?

 

[Malwina]

If you are looking for a sharp dividing line between a precessing rotation and a rotating fall, I do not believe that there is one.

This article on nutation shows at least some of the complexity lurking here.

Thanks for the link! I thought the gyroscope eventually fell down because its angular momentum was too small. If it is not the case, what changes in its mechanics between the moment when the gyroscope precesses and the moment when it falls?

 

[berkeman]

Yes, I am using this gyroscope and I am putting the end shown on the second photo directly on the surface with no support structure. I think I can calculate the distance it covers by calculating the precession of the top, because they move the same?

Did you record how many times the overall gyroscope's supporting structure rotated during the experiment for the different surfaces? On a low-friction surface, the gyroscope's supporting structure may rotate pretty freely, and hence not affect the actual spinning part much. On a high-friction surface, the supporting structure may rotate slowly, implying that there is increased drag on the internal rotating part...

 

[haruspex]

@Malwina, I'm unsure whether finding the minimum energy is your primary aim or just part of determining the rate of energy loss.

If the latter, can you start the gyro at various known initial energies and chart the times to dropping? Assuming the drop is always at the same energy, the time differences will let you find the rate of energy loss. (I would expect this to be not constant because of drag.)

If the former, the above approach could still be used, but is likely to give poor accuracy because it involves calculating a small difference between pairs of large numbers.

From the theoretical side, here's my analysis:
The usual treatment of gyroscopes ignores the moment of inertia about diametral axes because almost all the angular momentum is about the principal axis. But as the spin rate drops, the precession rate increases (torque=$\vec\tau=\vec\Omega\times\vec L$), making the rotational energy about the diametral axis significant.
Taking that energy into account, with a rather crude calculation using $I_x=\frac 12I_z$ I found there is a minimum total energy at a given angle. This is probably not quite right, but for the axis tipped right over to the horizontal I got $\Omega^2=\sqrt 2\frac{\tau}{I}$, minimum energy $=mgh/\sqrt 2$, where h is the initial height of the mass centre.

 

[jbriggs444]

If it is not the case, what changes in its mechanics between the moment when the gyroscope precesses and the moment when it falls?

As I had suggested previously, there is no sharp dividing line. Just a continuum of conditions. The description as a precessing rotation becomes less and less apt as the rotation rate decreases.

 

[Malwina]

If the latter, can you start the gyro at various known initial energies and chart the times to dropping?

Oh, that's a great idea, thank you so much!

using Ix=12Iz I found there is a minimum total energy at a given angle. This is probably not quite right, but for the axis tipped right over to the horizontal I got Ω2=2τI, minimum energy =mgh/2

Could you be so kind as to explain where you got these formulas from?

 

[Malwina]

Did you record how many times the overall gyroscope's supporting structure rotated during the experiment for the different surfaces? On a low-friction surface, the gyroscope's supporting structure may rotate pretty freely, and hence not affect the actual spinning part much. On a high-friction surface, the supporting structure may rotate slowly, implying that there is increased drag on the internal rotating part...

I unfortunately did not. Do you think repeating the experiment and measuring this would be beneficial to my investigation?

 

[berkeman]

Do you have a sense for how much the structure rotated? You could just do a spot check on the two extremes (longest lasting run versus the quickest tip-over) to see if it looks like structure rotation might be a contributing factor.

 

[haruspex]

Could you be so kind as to explain where you got these formulas from?

It is reasonable to take the case where the axis has tipped over to horizontal and the KE is at its minimum to sustain that as being the end point.

The KE involved in the spin about the axis is $\frac 12 I_z\omega^2$. That associated with the precession is $\frac 12(I_x+mh^2)\Omega^2$. (I forgot the $mh^2$ previously, so this will get a different result.)
I assume $I_x=\frac 12I_z$, as for a disc, so I'll simplify $I_z$ to just $I$.

The two angular rates are related by $I\omega\Omega=\tau=mgh$.
This allows us to write the total KE as a function of one of the rotation rates (choose either) then differentiate to find the value of that rate which requires the least total KE.

 

[Malwina]

Do you have a sense for how much the structure rotated? You could just do a spot check on the two extremes (longest lasting run versus the quickest tip-over) to see if it looks like structure rotation might be a contributing factor.

Wow! I did just that and on the high friction surface (carpet) it made only 17 turns and on the low friction (glass) it was 41. I think I will re-do the experiment starting the gyroscope at different known energies, as haruspex sugested, to measure the rate at which energy loss occurs.

 

[Malwina]

That associated with the precession is ##\frac 12(I_x+mh^2)

I understand you used the parallel axis theorem, but I do not get how the diametric axis could be parallel to the principal axis, I thought they were perpendicular?

 

[haruspex]

I understand you used the parallel axis theorem, but I do not get how the diametric axis could be parallel to the principal axis, I thought they were perpendicular?

Because I consider the case where the gyroscope axis is tipped over to the horizontal, $I_x$ is about the vertical through the gyroscope’s centre. This is parallel to the precession axis, at horizontal offset h.

 

[Malwina]

The two angular rates are related by $I\omega\Omega=\tau=mgh$.

One last thing, in my work I need to have a source for the formulas used. I have searched in my textbooks and online ones that I found but I cannot find any that would relate these angular rates in this way. Do you happen to know where I should look for such a source?

 

[haruspex]

One last thing, in my work I need to have a source for the formulas used. I have searched in my textbooks and online ones that I found but I cannot find any that would relate these angular rates in this way. Do you happen to know where I should look for such a source?

It is given at https://en.wikipedia.org/wiki/Precession#Classical_(Newtonian), but the essential equation is $\vec \tau=\vec\Omega\times \vec L$. I found that at https://readingfeynman.org/tag/gyroscope/.

 

[Malwina]

It is given at https://en.wikipedia.org/wiki/Precession#Classical_(Newtonian), but the essential equation is $\vec \tau=\vec\Omega\times \vec L$. I found that at https://readingfeynman.org/tag/gyroscope/.

Thank you so much! The readingfeynman article is very helpful

 

[Malwina]

Hi to everyone reading this, I devised the following calculations. Could someone confirm if I understand the subject correctly and if my theoretically predicted angular precession velocity has a reasonable value? In the experiment I measured it to be twice as big. Can this be explained as KE decreasing due to friction etc. causing angular velocity to decrease and so angular precession velocity to increase?

 

[haruspex]

Hi to everyone reading this, I devised the following calculations. Could someone confirm if I understand the subject correctly and if my theoretically predicted angular precession velocity has a reasonable value? In the experiment I measured it to be twice as big. Can this be explained as KE decreasing due to friction etc. causing angular velocity to decrease and so angular precession velocity to increase?

You are assuming all the energy goes into $\omega$, but as the gyroscope tilts over more and more of it goes into $\omega_p$. Both that and frictional losses reduce $\omega$, making $\omega_p$ larger.

Also, you originally asked for the minimum energy. How do you know your procedure achieves that? E.g., if you set the gyro horizontal to begin with, the higher the initial spin rate the slower the precession rate (and the higher the total energy).
My guess is that at minimum energy the two rotation rates would be the same order of magnitude. Did you do the analysis I proposed in post #14?

 

[Malwina]

I did the analysis and I got Emin=0.052J at ω=26.26rad/s and ωp=16.6rad/s so they are as you said of the same order of magnitude. Correct me if I'm wrong: At the very first instant all energy goes to ω and then gradually transfers to ωp. I can make a video of the gyroscope spinning and manually record the times at which it's outer structure (namely the tip) completes the full rotation (2πrad). From that I can calculate how the precessional velocity changes overtime and compare it to the predicted value. If I initially set the gyro horizontally, will the minimal energy point be signified as the gyroscope falling off the support structure, i.e. below the horizontal? That would be convenient, because I would be able to calculate how much time it took for the gyroscope to lose it's energy.

 

[haruspex]

I did the analysis and I got Emin=0.052J at ω=26.26rad/s and ωp=16.6rad/s so they are as you said of the same order of magnitude. Correct me if I'm wrong: At the very first instant all energy goes to ω and then gradually transfers to ωp. I can make a video of the gyroscope spinning and manually record the times at which it's outer structure (namely the tip) completes the full rotation (2πrad). From that I can calculate how the precessional velocity changes overtime and compare it to the predicted value. If I initially set the gyro horizontally, will the minimal energy point be signified as the gyroscope falling off the support structure, i.e. below the horizontal? That would be convenient, because I would be able to calculate how much time it took for the gyroscope to lose it's energy.

The point at which it falls off the support depends largely on the details of the support, so I don’t see it as significant. E.g. if the tip of the gyroscope is a small ball, sitting on a tiny cup that can rotate freely, the gyroscope could go well below the horizontal. In the extreme, it ends up vertical again, the KE of the precession having gone back into axial spin.

 

[Malwina]

Okay, I understand. Would it make sense for me to then record the time after it falls off the structure until the internal spinning stops completely? After this point there would be no KE in the gyro.

 

[haruspex]

Would it make sense for me to then record the time after it falls off the structure until the internal spinning stops completely?

Doesn’t make sense to me.
The trouble is that your stated aim, finding the min KE that it does not fall off, is not well defined. As I wrote, it depends on the details of the support.
Were you given this task or did you make it up? If the latter, I suggest taking precessing at the horizontal as the end point.

 

[Malwina]

Were you given this task or did you make it up? If the latter, I suggest taking precessing at the horizontal as the end point.

I made it up, my project is "how does the energy in a gyroscope change with time" but now I understand why my approach does not give appropriate results. By "end point" do you mean I should assume it is at minimum energy then? I do not understand how I would be able to calculate energy loss otherwise. I can calculate (from the recordings) ωp at any time, but ω only at the initial point.

 

[haruspex]

I can calculate (from the recordings) ωp at any time, but ω only at the initial point.

You can use the precession equation to deduce $\omega$ from $\omega_p$ and the torque.

 

[Malwina]

Thank you for your continued help! I think there is a problem in my calculations, because my internal disc has a different orientation than the one on the attached image. (I also attached a photo of my gyro). That would make the initial axes of both spin and of precession vertical and parallel (even the same, I think) and at the end point they would be perpendicular (precession about the vertical and spin about the horizontal).

The KE involved in the spin about the axis is $\frac 12 I_z\omega^2$. That associated with the precession is $\frac 12(I_x+mh^2)\Omega^2$. (I forgot the $mh^2$ previously, so this will get a different result.)
I assume $I_x=\frac 12I_z$, as for a disc, so I'll simplify $I_z$ to just $I$.

I cannot crack how that would affect these formulas. Do I disregard the +mh^2?

 

[hutchphd]

I cannot crack how that would affect these formulas. Do I disregard the +mh^2?

Feynman does a good job on precession. In particular fig. 20-6 and its environs.

 

[Malwina]

Feynman does a good job on precession. In particular fig. 20-6 and its environs.

Okay, I understand how the equations for new Torques are derived. Does moment of inertia (I) work analogously, because τ = Iα, so
Iz′=Iz
Ix′=Ixcosθ+Iycosθ
Iy'=Iycosθ-Ixsinθ?

 

[hutchphd]

The moment of inertia is fixed (in the frame of reference attached to the body). It is a matrix that is diagonal in the coordinate system that recognizes the symmetry of the body. Those are the body coordinates usually chosen. Your question is rather general.....I do not know what you need here, please be specific.

 

[Malwina]

Generally, I want to calculate the energy loss in the gyroscope overtime. To do that I did the evaluation of the dependency of KE on ωp as haruspex sugested in #14. Now I realized that there might be a problem with the formulas, as I think the spin axis and precession axis are not parallel, but perpendicular at the end point (when the gyroscope tipped to the horizontal). Now I'm looking for a way to incorporate this into the formula for KE associated with precession, but I do not know how.

Basically, I am looking for a formula relating KE with ωp.

 

[Malwina]

Oh! Nevermind! I misunderstood what the parallel axis theorem refered to. It is not the spin and precession axes that are parallel, but spin about the side of the disc and the spin about the centroid of the disc. The formulas work then, thank you.

My new idea is to put the gyroscope at the horizontal initially and since I found a function expressing KE as a function of ωp, I can calculate KE at different times by measuring ωp.