Minimize Total Length of Cables: Estimate Minimum Value?

[MarkFL]

Here is the question:

How to estimate the minimum value?

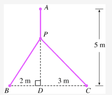
A point P needs to be located somewhere on the line AD so that the total length L of cables linking P to the points A, B, and C is minimized (see the figure). Estimate the minimum value of L to two decimals.

View attachment 2123

So far I have:

dL/dx=1 + ((x-5)/(sqrt(29-10 x+x^2))) + ((x-5)/(sqrt(50-10 x+x^2)))

What is the next step??

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Lavender V,

Let's let $0\le x\le 5$ represent the length of segment $\overline{DP}$ in meters. And so the total length of cable as a function of $x$ is then obtained via the Pythagorean theorem as:

$$L(x)=(5-x)+\sqrt{x^2+2^2}+\sqrt{x^2+3^2}$$

Now, we may differentiate with respect to $x$ and equate the result to zero to obtain the critical value(s):

$$L'(x)=-1+\frac{x}{\sqrt{x^2+4}}+\frac{x}{\sqrt{x^2+9}}=0$$

Now, since we are thankfully allowed to approximate, we may use Newton's method here to approximate the root of this equation.

Let:

$$f(x)=-1+\frac{x}{\sqrt{x^2+4}}+\frac{x}{\sqrt{x^2+9}}$$

We need to compute the first derivative, and so for the last two terms, consider:

$$g(x)=\frac{x}{\sqrt{x^2+k}}$$

Using the quotient, power and chain rules, we obtain:

$$g'(x)=\frac{\sqrt{x^2+k}(1)-x\dfrac{x}{\sqrt{x^2+k}}}{\left(\sqrt{x^2+k} \right)^2}=\frac{k}{\left(x^2+k \right)^{\frac{3}{2}}}$$

And so we may conclude that:

$$f'(x)=\frac{4}{\left(x^2+4 \right)^{\frac{3}{2}}}+\frac{9}{\left(x^2+9 \right)^{\frac{3}{2}}}$$

Newton's method gives us the recursion:

$$x_{n+1}=x_{n}-\frac{f\left(x_n \right)}{f'\left(x_n \right)}$$

And so using the definition of $f$ and its derivative, we have:

$$x_{n+1}=x_{n}-\frac{-1+\dfrac{x_n}{\sqrt{x_n^2+4}}+\dfrac{x_n}{\sqrt{x_n^2+9}}}{\dfrac{4}{\left(x_n^2+4 \right)^{\frac{3}{2}}}+\dfrac{9}{\left(x_n^2+9 \right)^{\frac{3}{2}}}}$$

Now, using a computer or CAS, and $x_0=1$, we find:

$$x_1\approx1.36825580018177$$

$$x_2\approx1.40658793851904$$

$$x_3\approx1.40699724822532$$

$$x_4\approx1.40699729457262$$

$$x_5\approx1.40699729457262$$

This is accurate to 15 digits, more than enough to get an approximation for the minimum of $L$ to two decimal places. Now, if we note that:

$$f'(x)=L''(x)>0$$

For all real values of $x$, then by the second derivative test, we may conclude that this critical value is at the global minimum, and we need not check the boundaries.

Thus, we may conclude:

$$L_{\min}\approx L(1.40699729457262)\approx9.35\text{ m}$$