Minimum Speed of a Rock: Solving Problem with Pit Gap of 40m

[surfhare75]

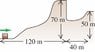
Here is the Problem. A 2.8-kg block slides over the smooth, icy hill shown in the figure .The top of the hill is horizontal and 70 m higher than its base. i attached the Figure Below.


What minimum speed must the block have at the base of the hill so that it will pass over the pit at the far side of the hill without falling into it?

I tried using .5mv1^2+m1gH=.5mv2^2+m2gH but I need to know the gap between the pit which is 40m. I believe I use H=.5gt^2 to find the time and use projectile motion x=vosin(x)t to find the distance.

 

[Bill Foster]

I can't see the picture.

Is the hill curved?

 

[surfhare75]

The picture should be loaded now, but in the picture the hill is curved but does not seem to be stated specially. This is from a chapter on potential and conservation energy

 

[Bill Foster]

Cant' see it. It says: "Attachments Pending Approval"

 

[azatkgz]

I also cannot see figure.

 

[azatkgz]

I think if the top of the hill is horizontal,then we can use

$$x=v_{top}t$$

$$y=\frac{1}{2}gt^2$$

 

[james brug]

The solution to this should be the initial velocity it takes to get to top of the hill plus the velocity needed to clear the pit, right? I get about 56.8 m/s which is apparently wrong.

$$\sqrt{1372}\;m/s+19.8\;m/s$$

 

[james brug]

Can someone please help ?

 

[james brug]

I have found the answer.

 

[Duncan1382]

I'm not sure if this is right, but this is what I came up with:

1) I found the speed that the object needed to be going to clear the jump.. not too hard. I assumed the ground was horizontal at the launch angle.
2) I used Energy to solve the problem.

Speed to Clear:
$$\Delta$$y = .5at²
-20m = -4.9$$m/s$$²t²
t = 2.02 seconds

no wind resistance = no acceleration

v = delta x / t = 40m / 2.02s = 19.80m/s

--
E_top = E_bottom

2.8kg(g)(70m) + .5(2.8kg)(19.8$$m/s$$)² = .5 (2.8kg)v²
v = 42.00$$m/s$$

 

[james brug]

Yes, that is correct.


$$\sqrt{1372\;m^2/s^2+(19.8\;m/s)^2}$$= Life, the Universe, and Everything