Minimum Velocity Required for Loop-The-Loop Problem

[JackFyre]

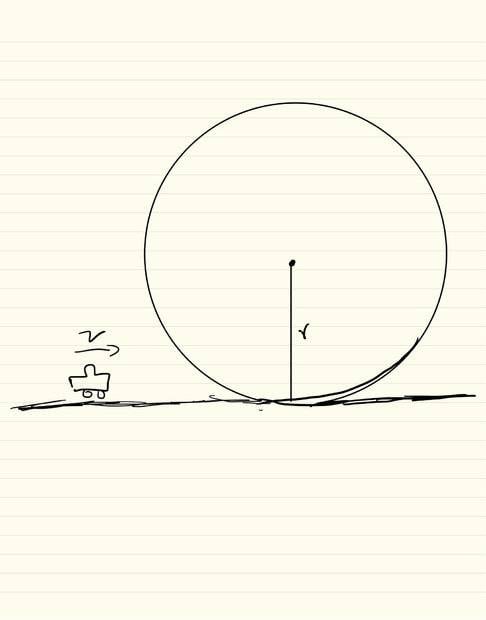
A question regarding the minimum velocity required by a particle to 'do a loop' without falling-

Assuming the particle has a velocity v before reaching the loop. Then-
KE = mv²/2, at the bottom of the loop.

potential energy at the top-most point of the loop= 2mgr (2r = h)
then, by the law of conservation of energy, mv²/2 = 2mgr, and we get v = 2√gr
in this case, the particle will have zero kinetic energy at the the top of the loop, an will fall, as it has 0 velocity. However, if the initial velocity were slightly higher, say v+Δv, then the particle will have some velocity a the top of the loop.

By this logic, should not the minimum velocity for a particle to safely complete a loop be just a little more than 2√gr ?

 

[erobz]

In order for the particle to complete the loop, the normal force from the track onto the particle must be nonzero.

Do you see what that implies for the minimum velocity ( and hence kinetic energy ) the particle must have at the top of the loop?

 

[kuruman]

. . . by the law of conservation of energy, mv²/2 = 2mgr, and we get v = 2√gr
in this case, the particle will have zero kinetic energy at the the top of the loop, an will fall, as it has 0 velocity.

The particle will lose contact with the track before it reaches the top. When that happens, it will describe a parabolic trajectory inside the loop and land on the opposite side of the track. The kinetic energy will never go to zero. Reaching zero KE could be the case if one had a bead on a ring that is constrained to stay on the circle and the normal force is allowed to change direction from radially in to radially out.

 

[JackFyre]

The particle will lose contact with the track before it reaches the top. When that happens, it will describe a parabolic trajectory inside the loop and land on the opposite side of the track. The kinetic energy will never go to zero. Reaching zero KE could be the case if one had a bead on a ring that is constrained to stay on the circle and the normal force is allowed to change direction from radially in to radially out.

Thanks, that clears it up!