Redwaves
- 134
- 7
- Homework Statement
- At t=0 A is moving
At t = -1/3 ms B is at 300km north and send a light beam
Draw the Minkowski diagram then tell if the light beam will reach A
- Relevant Equations
- ##-\frac{1}{3} ms = -\frac{10^{-3}}{3}s##
##300km = 3\cdot10^5 m##
##ct = -\frac{10^{-3}}{3}s \cdot c##
I drew the Minkowski diagram, but I'm not sure if this is correct.
From what I drew the angle between x and ct ##\approx 0##
then the event is "inside" the light ray and will eventually reach A.
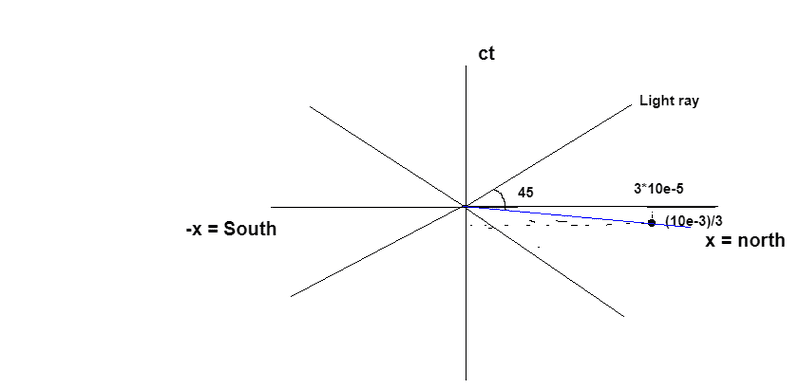
From what I drew the angle between x and ct ##\approx 0##
then the event is "inside" the light ray and will eventually reach A.