Minkowski Spacetime 3+1 Dimensions: Conformal Diagram w/Boundary

[Demystifier]

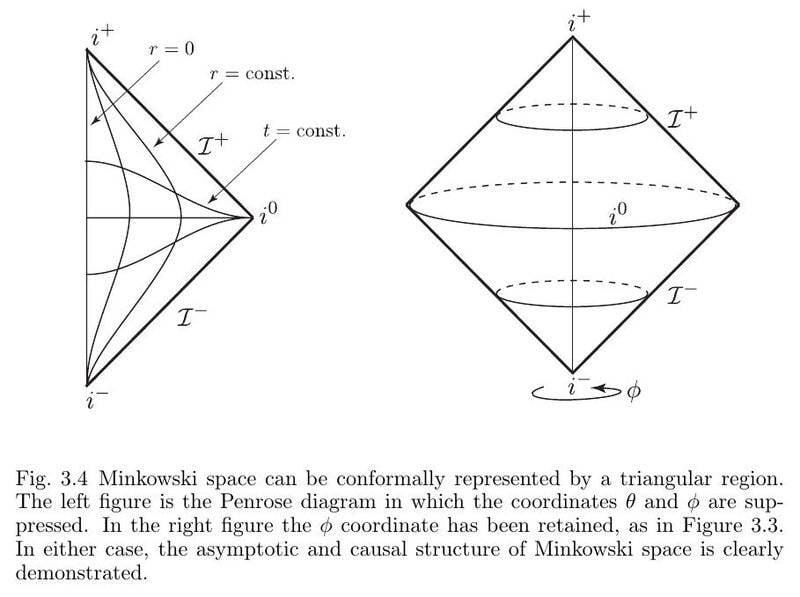
The Minkowski spacetime in 3+1 dimensions does not have a boundary. Yet, its conformal diagram (see the left diagram in the attached picture) has a timelike boundary $r=0$. A spacetime with a timelike boundary (another example is AdS) has a different causal structure than a spacetime without a boundary. Hence it seems that the conformal diagram of a spacetime may have a different causal structure than the original spacetime. Do I miss something?

 

[martinbn]

Why do you call $r=0$ a boundary?

 

[vanhees71]

Maybe you refer to maps of the Minkowski manifold, and generally any map covers only part of Minkowski spacetime. To cover the entire manifold you need an atlas with more than one (compatible) maps.

 

[Ibix]

The $r=0$ line isn't a boundary, it's a coordinate singularity. Worldlines reaching $r=0$ would be represented on the diagram as "bouncing off" the left hand edge, assuming you're just supressing the angular coordinates.

 

[Demystifier]

The $r=0$ line isn't a boundary, it's a coordinate singularity. Worldlines reaching $r=0$ would be represented on the diagram as "bouncing off" the left hand edge, assuming you're just supressing the angular coordinates.

But then why the "boundary" of AdS really is the boundary? How to know the difference?

 

[Demystifier]

Why do you call $r=0$ a boundary?

Because the conformal diagram ends there? If this is too naive, then what's the correct way to distinguish a true boundary from an apparent one?

 

[Demystifier]

Maybe you refer to maps of the Minkowski manifold, and generally any map covers only part of Minkowski spacetime. To cover the entire manifold you need an atlas with more than one (compatible) maps.

But the conformal diagram is supposed to describe the whole spacetime. Perhaps it does not really describe the whole spacetime?

 

[PeterDonis]

what's the correct way to distinguish a true boundary from an apparent one?

Worldlines end on a boundary. Worldlines don't end at the timelike $r = 0$ line; as @Ibix says, they "reflect" there.

More technically, the "true boundary" on a Penrose diagram is a locus that is not part of the original spacetime; it is "added" as part of constructing the Penrose diagram, in order to help in analyzing worldlines that, in the original spacetime, "go to infinity".

 

[PeterDonis]

the conformal diagram is supposed to describe the whole spacetime.

More precisely, it describes the 2-space portion of the spacetime that is everywhere orthogonal to the 2-spheres. Penrose diagrams, at least in the usual form, are only constructible for spherically symmetric spacetimes. In most such cases, one Penrose diagram is sufficient to cover the entire 2-space and is not affected by the usual issue with 2-spheres that requires at least two charts to cover one.

 

[Demystifier]

Worldlines end on a boundary. Worldlines don't end at the timelike $r = 0$ line; as @Ibix says, they "reflect" there.

More technically, the "true boundary" on a Penrose diagram is a locus that is not part of the original spacetime; it is "added" as part of constructing the Penrose diagram, in order to help in analyzing worldlines that, in the original spacetime, "go to infinity".

Can you explain this on the example of AdS boundary? Do worldlines reflect from AdS boundary? Is AdS boundary a part of the original spacetime?

 

[Demystifier]

Penrose diagrams are only constructible for spherically symmetric spacetimes.

How about Kerr black hole?

 

[PeterDonis]

AdS boundary?

Do you have a reference for the Penrose diagram of AdS?

 

[Demystifier]

Do you have a reference for the Penrose diagram of AdS?

E.g.
https://arxiv.org/abs/1611.01118
Hawking and Ellis, page 132
as well as most introductions to AdS/CFT

 

[Ibix]

But then why the "boundary" of AdS really is the boundary? How to know the difference?

As far as I'm aware the boundaries are places where a coordinate "goes to infinity" or there's a curvature singularity. I don't think you can tell the difference between a boundary and an edge like $r=0$ a priori. You either have to hope someone's labelled it or follow through the coordinate transforms yourself.

I'm not really familiar with anti de-Sitter spacetime - from a glance it looks like there's meaning to negative $r$ coordinates, which is not the case in regular spherical polars on Minkowski spacetime.

 

[Antarres]

How about Kerr black hole?

For Kerr black hole, the conformal diagram that you construct is usually for constant $\theta$ section of the spacetime(often chosen to be simple, although in principle it doesn't have to be). Because the symmetry isn't spherical, you can't suppress both angles to create a 2 dimensional diagram that describes complete spacetime, although drawing a section already gives you quite a lot of information. What @PeterDonis meant I assume is just about suppressing dimensions on a drawing. If you don't have spherical symmetry, you can't suppress angles and treat points as 2-spheres.

 

[PeterDonis]

E.g.
https://arxiv.org/abs/1611.01118

I don't see any Penrose diagram in this paper.

Hawking and Ellis, page 132

Unfortunately I don't have my copy handy.

 

[PeterDonis]

How about Kerr black hole?

There isn't one single Penrose diagram for Kerr spacetime. You can pick a particular 3-surface (the two most common ones are $\theta = 0$ and $\theta = \pi / 2$) and make a "Penrose-like" diagram of that surface, where points in the diagram now represent circles instead of 2-spheres.

 

[martinbn]

Can you explain this on the example of AdS boundary? Do worldlines reflect from AdS boundary? Is AdS boundary a part of the original spacetime?

It is similar. The dotted line $r=0$ reflects. The other vertical line is infinity, which is timelike here.

 

[Demystifier]

It is similar. The dotted line $r=0$ reflects. The other vertical line is infinity, which is timelike here.

So the AdS vertical line is the boundary because it's at infinity, is it what you are saying? Does it mean that a boundary cannot be at a finite distance? What if I consider a truncated Minkowski spacetime, defined as Minkowski with a ball of radius $r_0$ removed? Now the line $r=r_0$ is a true boundary, and yet it is not at infinity.

 

[Demystifier]

I don't see any Penrose diagram in this paper.

Page 11.

 

[Demystifier]

Ah, I think I get it. For the 4-dimensional spacetime, a boundary must be 3-dimensional. If spacetime is spherically symmetric, then "any" point on Penrose diagram represents a sphere $S^2$. Hence $r=r_0$ represents a 3-dimensional submanifold, so if the diagram ends at $r=r_0$ for finite $r_0$, then it's a boundary.

However, the above is not valid for $r=0$. A point on Penrose diagram with $r=0$ does not represent a sphere. It's just a point, even from the 4-dimensional point of view. Hence $r=0$ is not 3-dimensional (it's only 1-dimensional, due to the extension in time), so it cannot be a boundary of the 4-dimensional spacetime.

 

[PeterDonis]

Page 11.

That isn't a Penrose diagram, although it's sort of like one. AdS is spherically symmetric, so a Penrose diagram for it would have each point representing a 2-sphere. That's not the case for the diagram on page 11 of the paper you referenced.

The right half of the diagram on page 11 would be a proper Penrose diagram, at least if I'm interpreting their notation correctly. The vertical line marked $\psi = 0$ should be marked $r = 0$ in the usual notation for spherically symmetric spacetimes and would behave like the $r = 0$ line in Minkowski spacetime, and the vertical line $\scri$ at the right edge would be the boundary at infinity (which is not actually part of the spacetime itself).

 

[PeterDonis]

For the 4-dimensional spacetime, a boundary must be 3-dimensional.

A point on Penrose diagram with $r = 0$ does not represent a sphere. It's just a point, even from the 4-dimensional point of view. Hence is not 3-dimensional

I think this is basically correct, yes.

 

[Demystifier]

I think this is basically correct, yes.

Good, so I think this solves my problem.