Modal amplitudes of circular plate

[trimboone]

Hi all,

I'm a final year acoustics student in the UK attempting to model the modal response of a circular plate as part of my thesis.

Essentially, i have this equation :

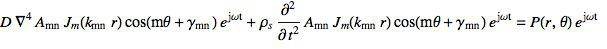
and I am trying to deal with the left term of the LHS.

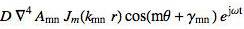
I'm trying to find out whether the full version of the biharmonic laplacian Jm(..)cos(..) can be expanded and factorised to be in terms of Jm(..) x cos(..) x (everythingelse!) as i am trying to solve the above equation for A_mn

In this form my theory will work but the actual derivation of the biharmonic laplacian using trigonometric functions and bessel functions together is killing me, I've already wasted a good 2 weeks trying this!

Can anyone help?

 

[jvicens]

Dear student,

First of all, congratulations on reaching the final year of your studies and taking on such a challenging topic for your thesis. The modal response of a circular plate is a complex and important area of study in acoustics, and it's great to see that you are tackling it head on.

In regards to your question about expanding and factorising the biharmonic laplacian, I can understand the frustration you are facing. This is a common problem faced by many researchers in the field, and it is not surprising that it has taken up a significant amount of your time.

I would suggest reaching out to your supervisor or other experts in the field for guidance and support. They may have valuable insights or resources that could help you in your derivation. Additionally, you could also consider consulting with other researchers or joining online forums to discuss your problem and potentially get some helpful advice.

In any case, it is important to remember that research and problem-solving can be a slow and challenging process, but the satisfaction of finding a solution is worth the effort. Keep persevering and don't hesitate to seek help when needed.

Best of luck with your thesis!