- #1
blamking
- 1
- 0
This is actually part of a much bigger goal, but I have isolated the problem I am having, which I have been struggling with for quite a while. I feel like the problem may be obvious to someone here.
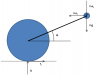
I attached a diagram of the problem to try to help illustrate it.
Assume there is a massless wheel (in the xy-plane) of radius R that can roll with no slip on a horizontal surface. Rigidly attached to the wheel at a distance L away from the center is a point mass, m. Only the wheel makes contact with ground. My goal is to find how this system acts over time.
Kinematic equations for relative acceleration
sum of forces = ma
sum of moments = Iα
Kinematic equations of particle rectilinear motion and rotation about a fixed axis.
N is the normal force between the ground and point of contact on the wheel. fx is the force of friction between the wheel and ground. θ is the angle between the x-axis and the vector between the center of the wheel and the point mass. I is the moment of inertia, ax and ay are the components of the acceleration of the point mass, α is the angular acceleration of the system, and ω is the angular velocity.
The following are my interpretation of the kinematic equations for relative acceleration, the sum of the forces, and the sum of the moments around the point mass. I then use these equations to solve for the linear and rotational accelerations, the normal force, and the friction force given the rest of the variables.
[itex]a_x+\alpha(R+Lsin(\theta))=-\omega^2Lcos(\theta)[/itex]
[itex]a_y-\alpha(Lcos(\theta))=-\omega^2Lsin(\theta)[/itex]
[itex]-ma_x+f_x=0[/itex]
[itex]-ma_y+N=mg[/itex]
[itex]-I\alpha-NLcos(\theta)+f_x(R+Lsin(\theta))=0[/itex]
Once I have these, I update. px and py are the coordinates of the point mass, and vx and vy are the components of the velocity.
[itex]p_{x_{k+1}} = p_{x_k} + v_{x_k}{\Delta}t+a_{x_k}{\Delta}t^2/2[/itex]
[itex]p_{y_{k+1}} = p_{y_k} + v_{y_k}{\Delta}t+a_{y_k}{\Delta}t^2/2[/itex]
[itex]\theta_{k+1} = \theta_k + \omega_k{\Delta}t+\alpha_k{\Delta}t^2/2[/itex]
[itex]v_{x_{k+1}} = v_{x_k}+a_{x_k}{\Delta}t[/itex]
[itex]v_{y_{k+1}} = v_{y_k}+a_{y_k}{\Delta}t[/itex]
[itex]\omega_{k+1} = \omega_k+\alpha_k{\Delta}t[/itex]
I then proceed to calculate the updated coordinates of the center of the wheel, which I'll call qx and qy.
[itex]q_x = p_x - Lcos(\theta)[/itex]
[itex]q_y = p_y - Lsin(\theta)[/itex]
This is where I run into problems. Logically, the wheel would retain the same y-coordinate between all time steps, since it is rolling on the ground. However, when I run my model for several time steps, it will leave the ground. Decreasing the time step decreases the magnitude of the problem, but never to the point where it is negligible. I've been thinking that since the rotation axis technically translates, the rotation kinematic equations might not be applicable in the form that I have them? Maybe I need to include Coriolis terms in my relative acceleration equations? It seems that everything I try only makes the problem worse, so i could really use some advice.
I also don't really want any huge reorganization of my approach to solving this problem unless there is no alternative, since, as I mentioned before, this is part of a bigger problem which is imposing some constraints on how I do things.
Anyway, thanks in advance, and please let me know if I need to clarify anything.
Homework Statement
I attached a diagram of the problem to try to help illustrate it.
Assume there is a massless wheel (in the xy-plane) of radius R that can roll with no slip on a horizontal surface. Rigidly attached to the wheel at a distance L away from the center is a point mass, m. Only the wheel makes contact with ground. My goal is to find how this system acts over time.
Homework Equations
Kinematic equations for relative acceleration
sum of forces = ma
sum of moments = Iα
Kinematic equations of particle rectilinear motion and rotation about a fixed axis.
The Attempt at a Solution
N is the normal force between the ground and point of contact on the wheel. fx is the force of friction between the wheel and ground. θ is the angle between the x-axis and the vector between the center of the wheel and the point mass. I is the moment of inertia, ax and ay are the components of the acceleration of the point mass, α is the angular acceleration of the system, and ω is the angular velocity.
The following are my interpretation of the kinematic equations for relative acceleration, the sum of the forces, and the sum of the moments around the point mass. I then use these equations to solve for the linear and rotational accelerations, the normal force, and the friction force given the rest of the variables.
[itex]a_x+\alpha(R+Lsin(\theta))=-\omega^2Lcos(\theta)[/itex]
[itex]a_y-\alpha(Lcos(\theta))=-\omega^2Lsin(\theta)[/itex]
[itex]-ma_x+f_x=0[/itex]
[itex]-ma_y+N=mg[/itex]
[itex]-I\alpha-NLcos(\theta)+f_x(R+Lsin(\theta))=0[/itex]
Once I have these, I update. px and py are the coordinates of the point mass, and vx and vy are the components of the velocity.
[itex]p_{x_{k+1}} = p_{x_k} + v_{x_k}{\Delta}t+a_{x_k}{\Delta}t^2/2[/itex]
[itex]p_{y_{k+1}} = p_{y_k} + v_{y_k}{\Delta}t+a_{y_k}{\Delta}t^2/2[/itex]
[itex]\theta_{k+1} = \theta_k + \omega_k{\Delta}t+\alpha_k{\Delta}t^2/2[/itex]
[itex]v_{x_{k+1}} = v_{x_k}+a_{x_k}{\Delta}t[/itex]
[itex]v_{y_{k+1}} = v_{y_k}+a_{y_k}{\Delta}t[/itex]
[itex]\omega_{k+1} = \omega_k+\alpha_k{\Delta}t[/itex]
I then proceed to calculate the updated coordinates of the center of the wheel, which I'll call qx and qy.
[itex]q_x = p_x - Lcos(\theta)[/itex]
[itex]q_y = p_y - Lsin(\theta)[/itex]
This is where I run into problems. Logically, the wheel would retain the same y-coordinate between all time steps, since it is rolling on the ground. However, when I run my model for several time steps, it will leave the ground. Decreasing the time step decreases the magnitude of the problem, but never to the point where it is negligible. I've been thinking that since the rotation axis technically translates, the rotation kinematic equations might not be applicable in the form that I have them? Maybe I need to include Coriolis terms in my relative acceleration equations? It seems that everything I try only makes the problem worse, so i could really use some advice.
I also don't really want any huge reorganization of my approach to solving this problem unless there is no alternative, since, as I mentioned before, this is part of a bigger problem which is imposing some constraints on how I do things.
Anyway, thanks in advance, and please let me know if I need to clarify anything.
Attachments
Last edited: