member 428835
Hi PF!
A circular cylinder contains an inviscid liquid, which is softly disturbed (i.e. velocities are small). There are no body forces, which implies the equilibrium free surface is that of a spherical cap with radius ##R## (see figure A). Inviscid implies we can assume potential flow, such that the liquid velocity ##V## can be expressed in terms of it's potential such that ##V = \nabla \psi##. The pressure throughout the liquid domain is ##P = -\nabla \psi## (recall velocities are small, so the non-linear term drops). The pressure at the free surface is governed by the Young-Laplace equation, which implies ##P \sim \sigma/R^2## there (actually this pressure term turns out to be VERY mathematically complicated, which is why I simply use the proportional notation). So the pressure balance at the free surface can be expressed by equating the two pressures at the interface.
Now let's assume the base of the cylinder is open such that flow can enter, shown in B). What is the pressure now in the liquid domain? I believe it is no longer ##P = -\nabla \psi##, but may also include a reservoir pressure from the inflow. How would you model this, given the small disturbance of the transient interface from equilibrium is some function ##\xi(x,y,z,t)##? There's a way I've been shown, but it doesn't intuitively make sense to me. Any help? Seems like @Chestermiller might know this one?
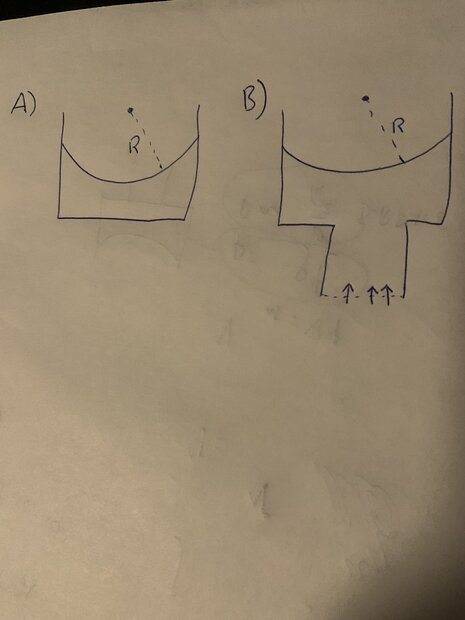
A circular cylinder contains an inviscid liquid, which is softly disturbed (i.e. velocities are small). There are no body forces, which implies the equilibrium free surface is that of a spherical cap with radius ##R## (see figure A). Inviscid implies we can assume potential flow, such that the liquid velocity ##V## can be expressed in terms of it's potential such that ##V = \nabla \psi##. The pressure throughout the liquid domain is ##P = -\nabla \psi## (recall velocities are small, so the non-linear term drops). The pressure at the free surface is governed by the Young-Laplace equation, which implies ##P \sim \sigma/R^2## there (actually this pressure term turns out to be VERY mathematically complicated, which is why I simply use the proportional notation). So the pressure balance at the free surface can be expressed by equating the two pressures at the interface.
Now let's assume the base of the cylinder is open such that flow can enter, shown in B). What is the pressure now in the liquid domain? I believe it is no longer ##P = -\nabla \psi##, but may also include a reservoir pressure from the inflow. How would you model this, given the small disturbance of the transient interface from equilibrium is some function ##\xi(x,y,z,t)##? There's a way I've been shown, but it doesn't intuitively make sense to me. Any help? Seems like @Chestermiller might know this one?