erobz
Gold Member
- 4,445
- 1,839
Edit: I've been catching errors I've made in the transcribing the formulas into latex ( not errors I made in the actual model..yet ). There may be more. I did this in one sitting.
I've been trying to model a bottle rocket (water propellant, compressed air fuel) and my model seems ok for a typical 2L soda bottle type dimension, but when I decrease the radius of the nozzle, I expect there to be a "maximum altitude" and then a decrease to "no altitude" for some small radius, but the model is showing otherwise. I can see that the velocity of the propellant goes right through the speed of sound as I decrease the nozzle radius, and I think this is the problem. I was hoping the shear force in the nozzle would prevent this issue, but it isn't doing the job. Below is the model (its a bit involved). I've tried to make sure I've explained it, but If I miss things, please let me know (that's why I'm posting it).
Figure 1 is the initial setup:
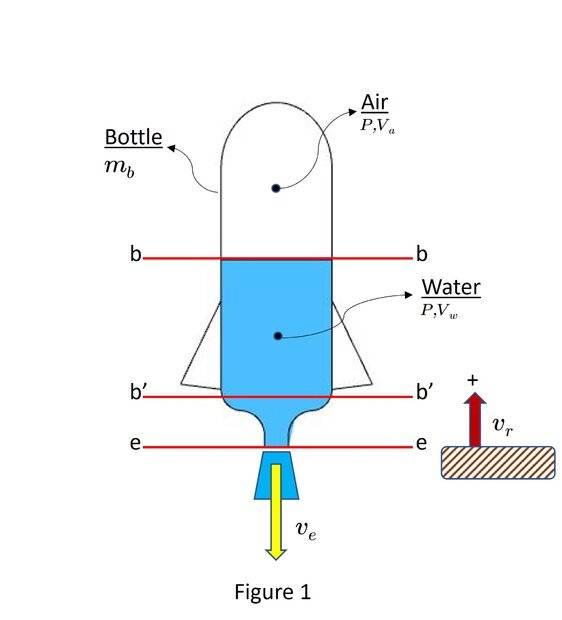
Initially there is some volume of air ## {V\llap{-}}_a## at a pressure ## P_o ## (gauge pressure). The volume of propellant ( water ) is ## { V\llap{-} }_w ## . Then at ## t = 0 ## the rocket is released. The velocity of the rocket ## v_r ## is w.r.t. a stationary frame fixed to the ground, and ## v_e ## is the velocity of the jet w.r.t. the rocket.
Figure 2 is the Free Body Diagram of the external forces acting on the rocket.
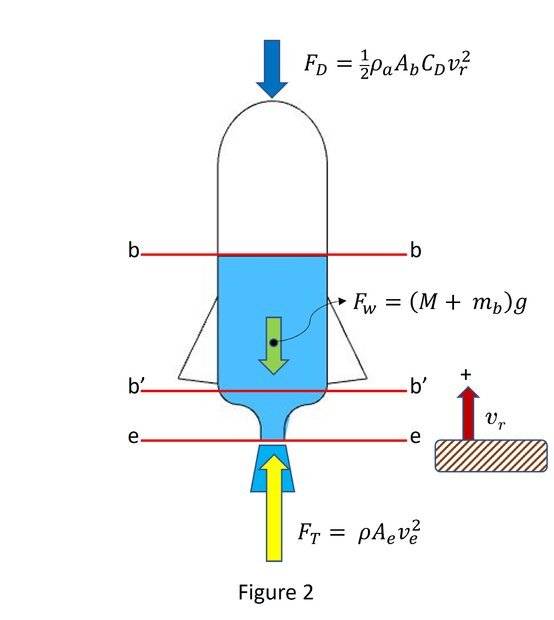
Section 1 - Applying Newton 2nd Law:
Assuming:
the weight of the air compressed air is negligible.
The fluid jet exits at ## P_{atm} ## (valid for fluid jet velocity that is less than the local speed of sound in the fluid)
$$ M_r \frac{d v_r}{dt} = -\dot{M} v_e - M_r g - \frac{1}{2} \rho_a A_b C_D v_r^2 $$
From here change independent variable from time ## t ## to mass of the propellant ##M## by noticing that:
$$ M_r = M + m_b \implies \dot{M_r} = \dot{M} = - \rho A_e v_e $$
Applying the Chain Rule:
$$ - M_r \rho A_e v_e \frac{d v_r}{d M_r} = \rho A_e v_e^2 - M_r g - \frac{1}{2} \rho_a A_b C_D v_r^2 \tag{1} $$
Section 2- ## v_e ## of Propellant:
Figure 3 shows a Force and Momentum diagram applied to the control volume shown by the dashed boundary.
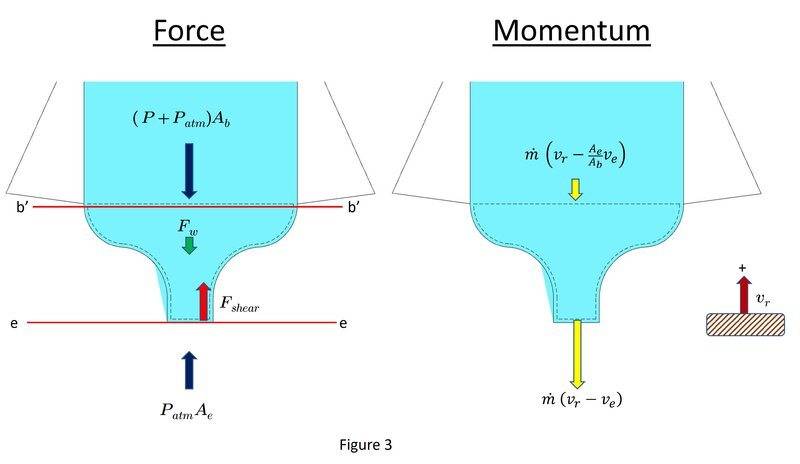
From the Reynolds Transport Theorem
$$ \sum F = \frac{d}{dt} \int_{cv} \rho \mathbf{v} dV\llap{-} + \int_{cs} \mathbf{v} \rho \mathbf{V} \cdot d \mathbf{A} $$
Assuming:
Uniform velocity across sections b'-b' and e-e
Continuity
The fluid in the control volume is incompressible $$ \sum F = m_{cv} \frac{d v_r}{dt} + \dot{m} v_{ee} - \dot{m} v_{b'b'} $$
Furthermore the mass in the control volume can basically be taken to be very small and I neglected the accumulation term.
$$ \sum F = \dot{m} \left( v_r - v_e \right) - \dot{m} \left( v_r - \frac{A_e}{A_b} v_e \right) $$
or substituting for ## \dot{m} ##
$$ \sum F = \rho A_e \left( \frac{A_e}{A_b} - 1 \right) v_e^2 $$
Force Balance:
Assuming:
Weight of mass in the control volume is negligible
Pressure in section b-b is equal to b'-b'
$$ \sum F = P_{atm} A_e - \left( P + P_{atm} \right) A_b - \pi D l \mu \left. \frac{dv}{dy} \right|_{r_o} $$
The last term on the right is the shear force, and the minus sign comes from the sign convention ( I think it correct ).
To get a functional slope ## \frac{dV}{dy}## at the boundary I had to assume a parabolic velocity distribution. *I'm aware that this somewhat contradicts an earlier assumption in applying the Reynolds Transport Theorem where I assumed uniform velocity distribution across the nozzle ( section e-e ).
Figure 4 shows this distribution.
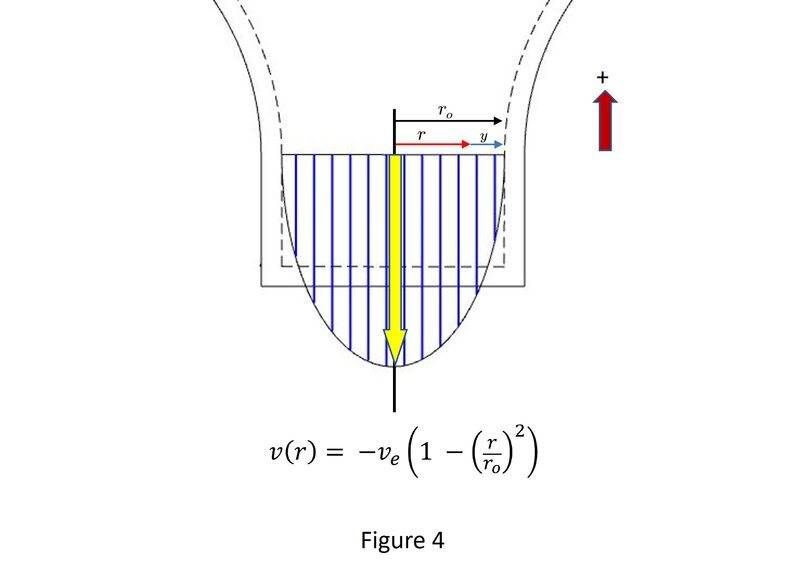
from this we have that:
$$ \left. \frac{dv}{dr} \right|_{r_o} = 2 v_e \implies \left. \frac{dv}{dy} \right|_{r_o} = -2 v_e $$
Substiting that result back in:
$$ \sum F = P_{atm} A_e - \left( P + P_{atm} \right) A_b + 4 \pi l \mu r_e v_e $$
Where:
## P ## is the gauge pressure of the compressed air
## \mu ## is the viscosity
## r_e ## is the exhaust radius
putting Section 2 all together:
$$ \rho A_e \left( \frac{A_e}{A_b} - 1 \right) v_e^2 = P_{atm} A_e - \left( P + P_{atm} \right) A_b + 4 \pi l \mu r_e v_e \tag{2} $$
Then solve the quadratic for ## v_e ##
$$ v_e = \frac{-b - \sqrt{ b^2 - 4 a c } }{ 2 a} $$
Where:
## a = \rho A_e \left( \frac{A_e}{A_b} - 1 \right) ##
## b = - 4 \pi l \mu r_e ##
## c = \left( P + P_{atm} \right) A_b - P_{atm} A_e ##
Section 3 - Isothermal Expansion of the Air
The last step before (1) is able to be numerically solved is to determine the pressure of the gas as a function of the mass of water in the bottle.
$$ \left( P_o + P_{atm} \right) {V\llap{-}_a}_o = \left( P + P_{atm} \right) { V\llap{-} }_a $$
Solving for ## P ##
$$ P = \left( P_o + P_{atm} \right) \frac{ {V\llap{-}_a}_o }{ V\llap{-}_a } - P_{atm} \tag{3}$$
Furthermore, we have that the total volume of the bottle ## V\llap{-} ## is fixed such that:
$$ \rho V\llap{-}_a = \rho V\llap{-} - M $$
Multiply the term on the left in (3) by ## \frac{\rho}{\rho} ##
$$ P = \left( P_o + P_{atm} \right) \frac{ \rho {V\llap{-}_a}_o }{ \rho V\llap{-} - M } - P_{atm} \tag{4} $$
So, you put that all together and solve (1) numerically for the EOM during powered flight ## v_r (M) ##.
To calculate the peak altitude:
its the powered flight altitude + the altitude from flight at burnout.

Getting this all down might have been more work than its worth... If I need to elaborate on my variables, derivations more let me know. It might take me a while to get the latex to parse so its readable
Thanks for any help, comments ect.. on what might be incorrect.
I've been trying to model a bottle rocket (water propellant, compressed air fuel) and my model seems ok for a typical 2L soda bottle type dimension, but when I decrease the radius of the nozzle, I expect there to be a "maximum altitude" and then a decrease to "no altitude" for some small radius, but the model is showing otherwise. I can see that the velocity of the propellant goes right through the speed of sound as I decrease the nozzle radius, and I think this is the problem. I was hoping the shear force in the nozzle would prevent this issue, but it isn't doing the job. Below is the model (its a bit involved). I've tried to make sure I've explained it, but If I miss things, please let me know (that's why I'm posting it).
Figure 1 is the initial setup:
Initially there is some volume of air ## {V\llap{-}}_a## at a pressure ## P_o ## (gauge pressure). The volume of propellant ( water ) is ## { V\llap{-} }_w ## . Then at ## t = 0 ## the rocket is released. The velocity of the rocket ## v_r ## is w.r.t. a stationary frame fixed to the ground, and ## v_e ## is the velocity of the jet w.r.t. the rocket.
Figure 2 is the Free Body Diagram of the external forces acting on the rocket.
Section 1 - Applying Newton 2nd Law:
Assuming:
the weight of the air compressed air is negligible.
The fluid jet exits at ## P_{atm} ## (valid for fluid jet velocity that is less than the local speed of sound in the fluid)
$$ M_r \frac{d v_r}{dt} = -\dot{M} v_e - M_r g - \frac{1}{2} \rho_a A_b C_D v_r^2 $$
From here change independent variable from time ## t ## to mass of the propellant ##M## by noticing that:
$$ M_r = M + m_b \implies \dot{M_r} = \dot{M} = - \rho A_e v_e $$
Applying the Chain Rule:
$$ - M_r \rho A_e v_e \frac{d v_r}{d M_r} = \rho A_e v_e^2 - M_r g - \frac{1}{2} \rho_a A_b C_D v_r^2 \tag{1} $$
Section 2- ## v_e ## of Propellant:
Figure 3 shows a Force and Momentum diagram applied to the control volume shown by the dashed boundary.
From the Reynolds Transport Theorem
$$ \sum F = \frac{d}{dt} \int_{cv} \rho \mathbf{v} dV\llap{-} + \int_{cs} \mathbf{v} \rho \mathbf{V} \cdot d \mathbf{A} $$
Assuming:
Uniform velocity across sections b'-b' and e-e
Continuity
The fluid in the control volume is incompressible $$ \sum F = m_{cv} \frac{d v_r}{dt} + \dot{m} v_{ee} - \dot{m} v_{b'b'} $$
Furthermore the mass in the control volume can basically be taken to be very small and I neglected the accumulation term.
$$ \sum F = \dot{m} \left( v_r - v_e \right) - \dot{m} \left( v_r - \frac{A_e}{A_b} v_e \right) $$
or substituting for ## \dot{m} ##
$$ \sum F = \rho A_e \left( \frac{A_e}{A_b} - 1 \right) v_e^2 $$
Force Balance:
Assuming:
Weight of mass in the control volume is negligible
Pressure in section b-b is equal to b'-b'
- No pressure loss from viscous effects in this section
- No pressure increase from hydrostatic pressure in the column
- No pressure increases from inertial forces associated with ## \frac{dv_r}{dt} ##
$$ \sum F = P_{atm} A_e - \left( P + P_{atm} \right) A_b - \pi D l \mu \left. \frac{dv}{dy} \right|_{r_o} $$
The last term on the right is the shear force, and the minus sign comes from the sign convention ( I think it correct ).
To get a functional slope ## \frac{dV}{dy}## at the boundary I had to assume a parabolic velocity distribution. *I'm aware that this somewhat contradicts an earlier assumption in applying the Reynolds Transport Theorem where I assumed uniform velocity distribution across the nozzle ( section e-e ).
Figure 4 shows this distribution.
from this we have that:
$$ \left. \frac{dv}{dr} \right|_{r_o} = 2 v_e \implies \left. \frac{dv}{dy} \right|_{r_o} = -2 v_e $$
Substiting that result back in:
$$ \sum F = P_{atm} A_e - \left( P + P_{atm} \right) A_b + 4 \pi l \mu r_e v_e $$
Where:
## P ## is the gauge pressure of the compressed air
## \mu ## is the viscosity
## r_e ## is the exhaust radius
putting Section 2 all together:
$$ \rho A_e \left( \frac{A_e}{A_b} - 1 \right) v_e^2 = P_{atm} A_e - \left( P + P_{atm} \right) A_b + 4 \pi l \mu r_e v_e \tag{2} $$
Then solve the quadratic for ## v_e ##
$$ v_e = \frac{-b - \sqrt{ b^2 - 4 a c } }{ 2 a} $$
Where:
## a = \rho A_e \left( \frac{A_e}{A_b} - 1 \right) ##
## b = - 4 \pi l \mu r_e ##
## c = \left( P + P_{atm} \right) A_b - P_{atm} A_e ##
Section 3 - Isothermal Expansion of the Air
The last step before (1) is able to be numerically solved is to determine the pressure of the gas as a function of the mass of water in the bottle.
$$ \left( P_o + P_{atm} \right) {V\llap{-}_a}_o = \left( P + P_{atm} \right) { V\llap{-} }_a $$
Solving for ## P ##
$$ P = \left( P_o + P_{atm} \right) \frac{ {V\llap{-}_a}_o }{ V\llap{-}_a } - P_{atm} \tag{3}$$
Furthermore, we have that the total volume of the bottle ## V\llap{-} ## is fixed such that:
$$ \rho V\llap{-}_a = \rho V\llap{-} - M $$
Multiply the term on the left in (3) by ## \frac{\rho}{\rho} ##
$$ P = \left( P_o + P_{atm} \right) \frac{ \rho {V\llap{-}_a}_o }{ \rho V\llap{-} - M } - P_{atm} \tag{4} $$
So, you put that all together and solve (1) numerically for the EOM during powered flight ## v_r (M) ##.
To calculate the peak altitude:
its the powered flight altitude + the altitude from flight at burnout.
Getting this all down might have been more work than its worth... If I need to elaborate on my variables, derivations more let me know. It might take me a while to get the latex to parse so its readable
Thanks for any help, comments ect.. on what might be incorrect.
Last edited: