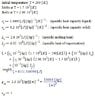Modelling the motion of a meteor

[PeterH]

Hi!
I am to model the motion of a meteor as it travels through the atmosphere, taking into account the loss of mass, which is 0.025 kg upon impact (height = 0). I also have to take into account the air resistance on the meteor, the fact that the air density is a function of height and that the orthographic projection of the meteor perpendicular the direction of movement (part of the air resistance equation) is a function of the mass of the meteor.
I assume that gravitational field strength is constant.

I have attached a picture of the equations I have been able to derive so far using standard formulas.

I have to solve the differential equations for x(t) and y(t), however, I have tried and failed and therefore seek help.

I can assure you that I am in no way trying to get out of doing some homework; this is for a very important school project and I really need help, so even the smallest hint would be greatly appreciated!
View attachment 3671

 

[zzephod]

You will need to do this numerically using the shooting method. You appear to have at least four undefined parameters: $c_D$, $\rho_m$, $\zeta$ and $m(0)$. One of these can be disposed of by assuming that you are interested only in high Reynolds numbers when $c_D\approx 1$ (see this). The shooting method uses only one, and in this case I presume that it should be $m(0)$. I think for your purposes you can assume that $\rho_m \approx 3$, or if you know what type it is you can use a better estimate (Google for it). Which leaves you with $\zeta$ to sort out and since I don't know what this represents I can't help with that.

You start by reformulating your equations as a first order system which is integrated numerically (with some guess at the initial mass) until $y=0$ then you record the residual mass at that time. Repeat with a different initial mass (adjusting your initial mass up of down depending on if the final mass was too high or too low).

Repeat until you get convergence using some sort of bisection method once you manage to bracket the initial mass.

Note: I don't think the equation for the mass as a function of time looks right, we would usually take $t=0$ to be the initial time, but then your initial mass will be zero. Also, you need to be careful of units, are the linear units metres or kilometres?

CB

 

[PeterH]

Thank you.

The only undefined parameter is m(0).
The linear units will be meters.

As for the rate of loss of mass, I have it from here:
1951ApJ...113..475C Page 475
I may have integrated it wrongly. Could it be that I'm missing a constant, m(0), in the equation?

ζ is the energy needed to vaporize 1 g of meteoric material from its inital temperature, which I have estimated to be 8.11 kJ. Depending on whether I will calculate mass in g or kg, I may use 8.11*10^3 kJ instead.View attachment 3672

 

[zzephod]

Thank you.

The only undefined parameter is m(0).

Then the shooting method should work.

CB

 

[blue_raver22]

Hello,

Thank you for sharing your project with me. It is always exciting to see young scientists working on real-world problems like modelling the motion of a meteor.

From the equations you have derived so far, it seems like you have a good understanding of the basic principles involved in this problem. As you mentioned, you will need to take into account the loss of mass, air resistance, and the changing air density as the meteor moves through the atmosphere.

To solve the differential equations for x(t) and y(t), you will need to use numerical methods such as Euler's method or Runge-Kutta methods. These methods involve breaking down the problem into smaller steps and using iterative calculations to approximate the solution. I would recommend consulting with your teacher or a mentor for guidance on how to apply these methods to your specific equations.

Additionally, it might be helpful to consider simplifying your equations by making some assumptions. For example, you could assume a constant air density and ignore the effects of air resistance, or you could assume a spherical shape for the meteor to simplify the calculation of the orthographic projection.

I hope this helps and I wish you the best of luck with your project. Keep exploring and learning, and don't be afraid to ask for help when you need it. That's what being a scientist is all about.

Best,