Moment of inertia (disk with off center hole)

[Imperitor]

I have a disk with some thickness to it and I need its moment of inertia.
So this is the formula with r1=0

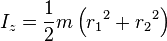
Now there is a "circular hole of diameter 'd' at a distance of 'r' from the geometric center of the disk." So I'm thinking that I should subtract the MoI of the hole from the disk. Here is a picture if you need it.

http://img99.imageshack.us/img99/782/50817033.jpg

I could use the same MoI equation as I did for the disk on the hole but that doesn't account for the hole being off centered. Any ideas??

I need to eventually equate this to a small mass rotating around a center point, so if there is a more direct approach please tell me. Thanks in advance for the help.

 

[tiny-tim]

Welcome to PF!

Hi Imperitor ! Welcome to PF!

I could use the same MoI equation as I did for the disk

That's right!

And then use the parallel axis theorem to find the moment of inertia about an axis not through the centre of mass.

 

[Imperitor]

Thanks. I really should have known that...

I'm really enjoying this forum. It's a great resource for an engineering student.

 

[Imperitor]

Wait a minute... hit another snag. To use that theorem I need to know what the mass of the missing hole is. I only know the mass of the disk as is (with the hole in it). Also the first formula I gave could only be used if I knew what the mass of the disk was with the hole filled in. This is driving me nuts. I can't even start working on the question I'm doing without getting this MoI.

 

[tiny-tim]

just got up… :zzz:

Wait a minute... hit another snag. To use that theorem I need to know what the mass of the missing hole is. I only know the mass of the disk as is (with the hole in it). Also the first formula I gave could only be used if I knew what the mass of the disk was with the hole filled in. This is driving me nuts. I can't even start working on the question I'm doing without getting this MoI.

Easy-peasy …

divide the given mass by the area, to give you the density …

then multiply by each area separately!