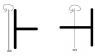Moment of inertia for composite objects

[vetgirl1990]

Homework Statement

Find the moment of inertia of these composite objects.

I've attached two different composite objects; each rod has length L and mass M.

Homework Equations

I = Icm + MD²
Long thin rod with rotation axis through centre: I_cm = 1/12ML²
Long thin rod with rotation axis through end: I_cm = 1/3ML²

The Attempt at a Solution

(a) For the image on the left:
I first found the total inertia of the objects: I_{cm total} = 1/12ML²
Then applied the Parallel Axis Theorem, because the composite object is rotating parallel to the actual axis of rotation: I = 5/12ML² + 2MD² (where D is the distance between the object's centre of mass and axis of rotation).
Feedback on this?

(b) For the image on the right:
Since one of the rods are going through the axis of rotation, I don't think I need to apply the Parallel Axis Theorem... So I just found the total inertia for both objects based on where their axis of rotation is.

I = I_{CM axis through centre} + I_{CM axis through end}
= 1/12ML² + 1/3M(L/2)²
= 1/12ML² + 1/3ML²/4
= 1/6 ML²

 

[gneill]

Can you give some more details about your determination of the $I_{cm}$ for the first image? I don't see how it turns out to be the same as that of a single rod about its center.

 

[J Hann]

You shouldn't need to use the parallel axis theorem for either situation.
For part (b), aren't all points on the vertical thin rod at a distance of L/2 from the axis of rotation;
or in other words where is the center of mass of the vertical rod in part (b)?