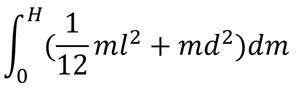Moment of inertia of a cuboid parallel to one of its faces (repost with diagram)

[eddiezhang]

Homework Statement

Knowing the mass moment of inertia of the 2d rectangle (the first picture), can I find an expression for the 3d cuboid (second picture) about some axis?

Relevant Equations

Parallel axis theorem: I_n = I + md^2

Hi all – this is a repost of an old question I had that was phrased quite poorly, so I hope some pictures help clarify what I was asking for.

I understand how the mass moment of inertia of a rectangle rotating about its width axis (=(1/12)mL^2) is derived by integrating with respect to mass. I will denote this I_y, and the 'y' axis is shown in the first attached picture (though obviously the actual axis of rotation is arbitrary and it's not that important what letter I assign it).

Question 1 - if the axis of rotation moves to n, would I be correct in saying that, by the parallel axis theorem, the new moment of inertia I_n = I_y + md^2 ?

Question 2 - knowing the expression for I_n for this 2d rectangle, is it possible to find to 'scale this up' (so to speak) and find I_n for the 3d cuboid (the first rectangle but just with height)? If so, how would you derive this result?

(both the rectangle and the cuboid have uniform density)

Thanks in advance - sorry for the repost, but I don't think I understood many of the replies to my first try

 

[haruspex]

Question 1 - if the axis of rotation moves to n, would I be correct in saying that, by the parallel axis theorem, the new moment of inertia I_n = I_y + md^2 ?

Yes.

Question 2 - knowing the expression for I_n for this 2d rectangle, is it possible to find to 'scale this up' (so to speak) and find I_n for the 3d cuboid (the first rectangle but just with height)?

Not simply.
Collapse the cuboid down to a 2D rectangle normal to the axis of interest. Each of the (infinitesimally thick) collapsed rectangles has the same MoI about that axis, so you can find the MoI of one, taking it to be the mass of the whole cuboid.

 

[eddiezhang]

Yes.

Not simply.
Collapse the cuboid down to a 2D rectangle normal to the axis of interest. Each of the (infinitesimally thick) collapsed rectangles has the same MoI about that axis, so you can find the MoI of one, taking it to the mass of the whole cuboid.

Thanks, but I'm a little unsure how to set up this integral - a bit like this?

If so, I'm also unclear on what dm should be changed to for this to actually make sense

thanks for bearing with me

 

[haruspex]

Thanks, but I'm a little unsure how to set up this integral - a bit like this? View attachment 339661

If so, I'm also unclear on what dm should be changed to for this to actually make sense

thanks for bearing with me

I didn't actually say to do an integral, but if you wish:
$\int(\frac 1{12}l^2+ d^2)dm$.

 

[eddiezhang]

I didn't actually say to do an integral, but if you wish:
$\int(\frac 1{12}l^2+ d^2)dm$.

Sorry, doesn't that produce the equation for I_n = (1/12)mL^2 + md^2?

I meant the moment of inertia of the 3d shape... I assumed that summing the infinitesimally thin rectangles would be best done with an integral, but I don't really have the maths ability to set that up (am but a lowly 16 year old)

Thanks for bearing with me once again...

 

[haruspex]

Sorry, doesn't that produce the equation for I_n = (1/12)mL^2 + md^2? View attachment 339672
I meant the moment of inertia of the 3d shape... I assumed that summing the infinitesimally thin rectangles would be best done with an integral, but I don't really have the maths ability to set that up (am but a lowly 16 year old)

Thanks for bearing with me once again...

Sorry, I forgot you had defined d to be a specific distance in your diagram.
In post #2 I wrote

Collapse the cuboid down to a 2D rectangle normal to the axis of interest

Note the word "normal". That means the collapse you want is into the XZ plane.
What is the distance from your axis to the mass centre now?

 

[eddiezhang]

Sorry, I forgot you had defined d to be a specific distance in your diagram.
In post #2 I wrote

Note the word "normal". That means the collapse you want is into the XZ plane.
What is the distance from your axis to the mass centre now?

sqrt(d^2 + (H^2)/4)?

 

[haruspex]

sqrt(d^2 + (H^2)/4)?

Yes. So use that as the displacement of the axis from the mass centre.

 

[eddiezhang]

Yes. So use that as the displacement of the axis from the mass centre.

Forgive me if I'm being a bit slow (this is a new topic for me and my physics teachers aren't much use...) - like this? (Unsure about the limits of integration)

Don't I also need to define some density function in order to integrate with respect to L or H...?

Sorry for making you walk me through this so slowly, but I do really appreciate it...

 

[haruspex]

Forgive me if I'm being a bit slow (this is a new topic for me and my physics teachers aren't much use...) - like this? (Unsure about the limits of integration)
View attachment 339677

Don't I also need to define some density function in order to integrate with respect to L or H...?

Sorry for making you walk me through this so slowly, but I do really appreciate it...

If you have a body B of mass m, and you consider it made of elements of mass dm, you can integrate over the body: $\int_{B}dm=m$

 

[eddiezhang]

If you have a body B of mass m, and you consider it made of elements of mass dm, you can integrate over the body: $\int_{B}dm=m$

I've only done single-variable calculus, so what does 'integrating over the body' mean...?

 

[Orodruin]

Don't I also need to define some density function in order to integrate with respect to L or H...?

Generally when you have a mass integral over dm you can rewrite that as an integral over space, either using the density and dV ($dm = \rho\, dV$) or by building the mass in some other way (slabs of width dh, etc) with the appropriate expression for dm.

Let me make some advertisment for dimensional analysis here. This simply cannot be the correct expression because it has the wrong physical dimension. MoI has the physical dimension mass x length². This expression has physical dimension mass² x length².

 

[eddiezhang]

Generally when you have a mass integral over dm you can rewrite that as an integral over space, either using the density and dV ($dm = \rho\, dV$) or by building the mass in some other way (slabs of width dh, etc) with the appropriate expression for dm.


Let me make some advertisment for dimensional analysis here. This simply cannot be the correct expression because it has the wrong physical dimension. MoI has the physical dimension mass x length². This expression has physical dimension mass² x length².

I see...

 

[Orodruin]

I've only done single-variable calculus, so what does 'integrating over the body' mean...?

Split your body into smaller sub-bodies (such as infinitesimal slabs of width dh). Express the mass of each such sub-body as dm = f(h) dh and integrate over the appropriate range of h to get the full body.

 

[eddiezhang]

Split your body into smaller sub-bodies (such as infinitesimal slabs of width dh). Express the mass of each such sub-body as dm = f(h) dh and integrate over the appropriate range of h to get the full body.

My try (probably wrong): (using 'H' as the height and summing infinitesimally short slabs of height dH with width W and length L)

dm = ρdV = ρWLdH

hence the mass integral becomes

?

I don't get how this helps me find the moment of inertia...

 

[haruspex]

I've only done single-variable calculus, so what does 'integrating over the body' mean...?

I'll offer a slightly different way of looking at it.
If we cut the body into n little masses, $m_1,..,m_n$, with distances $r_1,..,r_n$ from the axis, then the moment of inertia is approximately $\Sigma_im_ir_i^2$. In the limit, as we make the masses progressively smaller towards zero, we can write that as an integral: $\int r^2dm$, where r is a function of the particular mass meant by dm.

 

[eddiezhang]

I'll offer a slightly different way of looking at it.
If we cut the body into n little masses, $m_1,..,m_n$, with distances $r_1,..,r_n$ from the axis, then the moment of inertia is approximately $\Sigma_im_ir_i^2$. In the limit, as we make the masses progressively smaller towards zero, we can write that as an integral: $\int r^2dm$, where r is a function of the particular mass meant by dm.

I'm just unclear on how to apply this mathematically (i.e. setting up the integral). Here's what I think the computation would look like based on how you were nudging me along, though I'm probably wrong:

 

[haruspex]

I'm just unclear on how to apply this mathematically (i.e. setting up the integral). Here's what I think the computation would look like based on how you were nudging me along, though I'm probably wrong:

View attachment 339683

There's potential for confusion there. The H inside the integral is a constant, whereas dH is playing the role of a variable.
It would be clearer to write.
$\rho WL\int_{h=0}^H(d^2+\frac 14H^2)dh$

But there are a couple of things wrong here.

The n axis is parallel to the y axis, so the slices are at different distances along W, not H:
$\rho HL\int_{w=0}^W(d^2+\frac 14H^2)dw$
This reduces, of course, to $\rho WLH(d^2+\frac 14H^2)=m(d^2+\frac 14H^2)$

Also, this integral is the term to add to the MoI about an axis through the centre in the y direction. You still need the expression for $I_y$ (with the y axis being through the centre of the block, not at the bottom as you drew it).
When we changed the collapse to be along the y axis, that made the y axis normal to the rectangles, so the MoI is no longer just $\frac 1{12}mL^2$. H must have an effect.
This is easily fixed. For any small element dm at (x,0,z) relative to the centre, its MoI for a rotation about the centred y axis is $dm(x^2+z^2)$. When we sum those, it's the same as summing $dmx^2$ and $dmz^2$ separately then adding, giving $m\frac 1{12}(L^2+H^2)$.

 

[eddiezhang]

There's potential for confusion there. The H inside the integral is a constant, whereas dH is playing the role of a variable.
It would be clearer to write.
$\rho WL\int_{h=0}^H(d^2+\frac 14H^2)dh$

But there are a couple of things wrong here.

The n axis is parallel to the y axis, so the slices are at different distances along W, not H:
$\rho HL\int_{w=0}^W(d^2+\frac 14H^2)dw$
This reduces, of course, to $\rho WLH(d^2+\frac 14H^2)=m(d^2+\frac 14H^2)$

Also, this integral is the term to add to the MoI about an axis through the centre in the y direction. You still need the expression for $I_y$ (with the y axis being through the centre of the block, not at the bottom as you drew it).
When we changed the collapse to be along the y axis, that made the y axis normal to the rectangles, so the MoI is no longer just $\frac 1{12}mL^2$. H must have an effect.
This is easily fixed. For any small element dm at (x,0,z) relative to the centre, its MoI for a rotation about the centred y axis is $dm(x^2+z^2)$. When we sum those, it's the same as summing $dmx^2$ and $dmz^2$ separately then adding, giving $m\frac 1{12}(L^2+H^2)$.

Thanks for the heads up on the notation

I'm in over my head because I don't really understand the second part.

Why isn't $\rho WL\int_{h=0}^H(d^2+\frac 14H^2)dh$ the moment of inertia $I_n$ of the solid? Aren't we summing all the MoIs of the individual lamina with width dw, height H and length L? Why is it necessary to add it to $I_y(centre of mass)$?

I'm gonna keep on saying it because I do mean it - thanks (genuinely) for bearing with me...

 

[haruspex]

Why isn't $\rho WL\int_{h=0}^H(d^2+\frac 14H^2)dh$ the moment of inertia $I_n$ of the solid? Aren't we summing all the MoIs of the individual lamina with width dw, height H and length L? Why is it necessary to add it to $I_y(centre of mass)$?

No, we only summed the bits due to the displacement of the axis from the rectangle's centre. Since that displacement was the same for all our rectangles, the integration was trivial.

For one such rectangle, mass dm, its MoI about its centre is $\frac 1{12}(L^2+H^2)dm$. The n axis is displaced $\sqrt{d^2+(\frac 12H)^2}$ from the mass centre, so its MoI about n is $(\frac 1{12}(L^2+H^2)+d^2+(\frac 12H)^2)dm$.
Integrating just turns dm into m.

 

[eddiezhang]

No, we only summed the bits due to the displacement of the axis from the rectangle's centre. Since that displacement was the same for all our rectangles, the integration was trivial.

For one such rectangle, mass dm, its MoI about its centre is $\frac 1{12}(L^2+H^2)dm$. The n axis is displaced $\sqrt{d^2+(\frac 12H)^2}$ from the mass centre, so its MoI about n is $(\frac 1{12}(L^2+H^2)+d^2+(\frac 12H)^2)dm$.
Integrating just turns dm into m.

OH OH OH

That's just the parallel axis theorem, right...?

and so the $I_n$ of the solid is (I'm gonna try finish off the problem):

 

[haruspex]

OH OH OH

That's just the parallel axis theorem, right...?

and so the $I_n$ of the solid is (I'm gonna try finish off the problem):
View attachment 339734

Yup.

 

[eddiezhang]

Yup.

THANK YOU SO MUCH

I'd give you a medal but I'm too broke to pay for shipping to Australia

 

[Lnewqban]

 

[eddiezhang]

View attachment 339737

Yep... kicked myself for not seeing it this entire time

 

[Lnewqban]

Yep... kicked myself for not seeing it this entire time

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/parax.html#pax

https://en.wikipedia.org/wiki/List_of_moments_of_inertia

We have one minimum value of rotational inertia when turning the cuboid about its center of mass.
We have an increased value when turning it about the y or the n axes.
Reason: we are still turning the cuboid about its center of mass while we are turning it about an axis far from the CM; therefore, the summation of both values.