vcsharp2003
- 913
- 179
- Homework Statement
- A disk of radius R and mass M is connected to a rod that is rotating about O. The rod is rotating about at an angular velocity of ##\omega## about O. What would be the moment of inertia of the rod+disk system about an axis through O and perpendicular to plane of rotation of the rod. Assume the rod is massless and the disk is not rotating about it's center of mass axis.
- Relevant Equations
- ##I=\frac {MR^2} {2}## for a disk about an axis through its cm and perpendicular to the disk
## I_o = I_{cm} + M R^2##
I have come up with two different approaches, but I'm not sure which one is correct since they give different answers.
We use the following equation to get the total moment of inertia.
##I_o## = moment of inertia of disk about O axis + moment of inertia of road about O axis
Approach 1:
Consider the disk as a particle at it's center of mass.
##I_o = M (5R)^2 + 0= 25 MR^2##
Approach 2:
We use parallel axis theorem to get moment of inertia of disk about O axis.
##I_o= \frac {MR^2} {2} + M (5R)^2 + 0 \\= \frac {51MR^2} {2}##
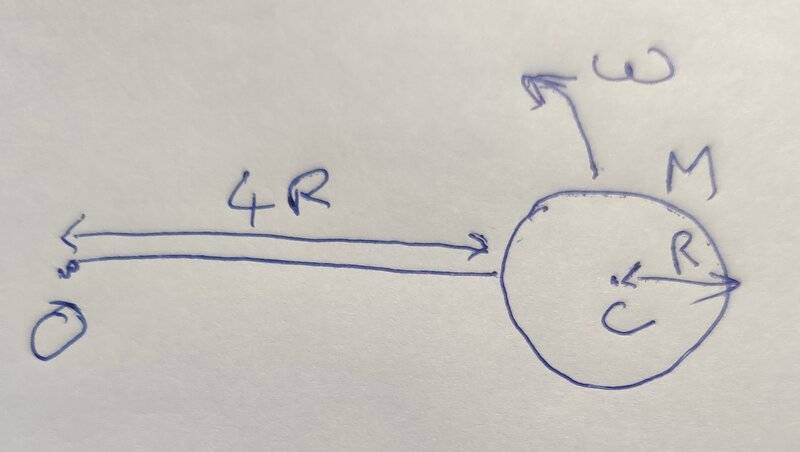
We use the following equation to get the total moment of inertia.
##I_o## = moment of inertia of disk about O axis + moment of inertia of road about O axis
Approach 1:
Consider the disk as a particle at it's center of mass.
##I_o = M (5R)^2 + 0= 25 MR^2##
Approach 2:
We use parallel axis theorem to get moment of inertia of disk about O axis.
##I_o= \frac {MR^2} {2} + M (5R)^2 + 0 \\= \frac {51MR^2} {2}##
Last edited: