Moment of Inertia of a Disk rotating around a rod

[thejinx0r]

Homework Statement

It's part of Kleppner and Kolenkow 7.4.
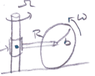
See the attached picture.
(The disk is rotating around the vertical "stick", not rotating towards it. (I have bad drawing skills)

The question mainly asks what is the normal force on the disk.

I am stuck trying to find the moment of inertia of the z direction.

Homework Equations

\int r^2 dm

The Attempt at a Solution

I don't have much to go with.

Well, I said that the perpendicular direction from the disk is constantly R.
For dm, I was thinking thinking of dividing the disc into vertical slices so that they look like horizontal rods.

Then I simply did not what to do because I did not know how to set up the bounds on the integral.

So, the mass of one those segments should be \rho dL with dL changing from 0 to 2b. and my integral should be times 2 since I have a top and bottom to my disk and from 0 to 2b is only one half.

But it just looked weird and I know it's wrong. So I really need help with this part.
\int_{0}^{2b} 2R^2 \rho LdL = 8R^2 \rho b^2

 

[Doc Al]

Take the easy road: Make use of the perpendicular axis theorem. (And then the parallel axis theorem.)

 

[thejinx0r]

Never head of the parallel axis theorem, will look it uo.

:D

 

[thejinx0r]

Actually, it is not making sens to me.
There must be something wrong I am doing.
Frrom the perpendicular axis theorem.

Iz_o =Ix+IyWe have
Ix= 1/2 mb^2.
Iy = 1/4 mb^2.
so, Iz _o = 3/4 mb^2.

Now, using the parallel axis theorem,
Iz=I_zo + mr^2
Iz = 3/4 mb^2 + mr^2.

Now I was interested at the angular momentum,
so L = I_z \Omega for the z component of the disc at that point
L = (3/4 mb^2 + mr^2.) \Omega
but
r\omega = R\Omega
so
L= 3/4 mb^2 \ Omega + 1/2 mb^2 \omega^2 \div \Omega

But somehow I found (on the interner) that it should be
1/4 mb^2 for Iz, which does work when I plug in the numbers... :S

Actually, it shouldn't matter what numbers I plug in, because i take the derivative of it which gives 0. But I would still like to know what I'm doing is right or wrong for calculating I.

 

[Doc Al]

Actually, it is not making sens to me.
There must be something wrong I am doing.
Frrom the perpendicular axis theorem.

Iz_o =Ix+Iy


We have
Ix= 1/2 mb^2.
Iy = 1/4 mb^2.
so, Iz _o = 3/4 mb^2.

For the disk, we know that Iz = 1/2 mb^2 and that Ix = Iy (by symmetry). Note that the z-axis (for now) is perpendicular to the plane of the disk.

See: Perpendicular Axis Theorem

 

[thejinx0r]

But the disk is upright, not flat.

So based on that diagram,
it's z would be my y.
x is x
and why would be z.

so, 1/2+1/4 = 3/4.

Hm,
but it does seem to give what I want if I do Iy=Iz-Ix.
But I highly doubt that it would be something I could do. :S

But at least if I just took Iy to begin with, it could explain a lot of things.

 

[Doc Al]

But the disk is upright, not flat.

So based on that diagram,
it's z would be my y.
x is x
and why would be z.

so, 1/2+1/4 = 3/4.

Did you read the link I gave?

Call the axes what you will, your equation should look like: I + I = 1/2 mb^2.

The I of the disk parallel to the z-axis but through its center of mass is 1/4mb^2 (per the above equation).

 

[thejinx0r]

I missed the in the plane part of

through the same point in the plane of the object.

Thanks a lot,
I will remember this.
I knew I missed something and made it sound really dumb