eddiezhang
- 39
- 8
- Homework Statement
- Consider a long rectangular prism with width w, height h and length l (a 'ruler' for brevity, although its height is non-negligible). The 'ruler' balances on a table with length l1 hanging off the side and l2 resting on the table. What is the ruler's moment of inertia if it starts to fall off the table?
- Relevant Equations
- Contained in attempt, and it's probably wrong too...
I'm sorry for a really basic question, but my physics class was just introduced to moments of inertia and I want to try find them in three dimensions
Attempt:
Step 1) Search up 'moment of inertia of a rectangle' and find this:
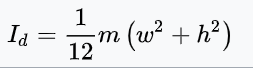
Step 2) Multiply by the height??? This is definitely wrong
Step 3) Realize I'm completely clueless and should ask a stranger onlineThanks...
Attempt:
Step 1) Search up 'moment of inertia of a rectangle' and find this:
Step 2) Multiply by the height??? This is definitely wrong
Step 3) Realize I'm completely clueless and should ask a stranger onlineThanks...