Moment of inertia (Perpendicular axis theorem)

[andyonassis]

Homework Statement

Find the moment of inertia of frustum perpendicular to axis of symmetry about the top with radius r and bottom with radius R

Relevant Equations

I = (3m/10)[(R^5-r^5)/(R^3-r^3)] (about axis of symmetry)

So i derived the moment of inertia about the axis of symmetry (with height h) and I am confused about the perpendicular axis theorem.
The problem ask to find the moment of inertia perpendicular to axis of symmetry

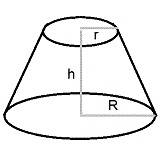
So the axis about h, i labelled as z, the two axis that are perpendicular to z, i labelled as x and y.
I already found $$I_{z} = (3m/10)\frac{(R^5-r^5)}{(R^3-r^3)]}$$
So according to perpendicular axis theorem,
$$I_z = I_x + I_y$$
and because of symmetry $$I_x = I_y$

So i derived a solution for Ix and Iy
$$Ix = I_y = (3m/20)\frac{(R^5-r^5)}{(R^3-r^3)]}$$
I'm confused as the theorem also says $$I_x = I_y+I_z$$ and $$I_y = I_x+I_z$$

 

[etotheipi]

Perpendicular axis theorem only applies to 2D lamina!