Moments of Inertia: Hi, Need Help Understanding?

[Gunter_ZA]

Hi,

I need some assistance understanding moments of inertia. I am doing some review for an upcoming exam, however I am slightly stumped by this question. I have already tried googling "moments of inertia" to try and understand the concept better, but I am having issues knowing when to apply which formulas.

I have attached my specific question and the "answer" to the question, hopefully someone can help me understand how to get the answer.

----

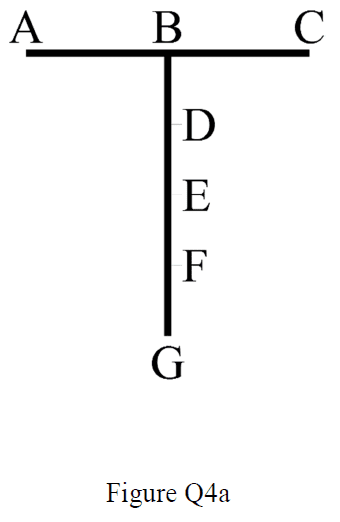
Two identical slender rods of length l and mass m are linked together at 90deg, as shown in figure Q4a (image attached), to form a link in a mechanism. Point B is midway between A and C, and points B, D, E, F and G are equally spaced along the lower link.

i) Determine the position of the center of gravity of the link

ii) Find the moment of inertia of the link about the point B

iii) Find the moment of inertia of the link about the point D

iv) Find the radius of gyration about the point G

---

ANSWERS:

i) Center of gravity is at D

ii) I_B=(5/12)ml² kg m²

iii) I_D=(7/24)ml² kg m²

iv) k= sqrt(17/24) l m

----

*My attempts*i)I know inherently that the centre of gravity is at D. How do i prove it mathematically?

----

ii)I get the moment of inertial about B like so:

I[subBb[/sub] = (ml²)/3 + ((ml²/3) - (ml²)/4)

But i don't understand why I am supposed to subtract. Is it because the centre of gravity is l/2 below B?

----
iii)For I_D I get the answer by doing:

I_D = ((ml²)/3 - (ml²)/4) + ((ml²)/(3*16)) + (9ml²)/(16*3)

Why do I subtract (ml²)/4) if that rod is above D?----

iv)I'm trying to use I_G to find the radius of gyration:

So for I_G

I_G = (7/24)ml² - ml²Here I am using the parallel axis theorem, but why do I subtract the (md²) of the AC rod from the Moment of inertia about D?

 

[haruspex]

the centre of gravity is at D. How do i prove it mathematically?

It is obviously on the line BG, but where? You seem to have forgotten how to find a mass centre. It is the point about which the net first moment is zero. E.g. in the y direction, if D is the mass centre then measuring the y_i offset of each element m_i from D you want Σy_im_i=0.

I get the moment of inertial about B like so:

I[subBb[/sub] = (ml2)/3 + ((ml2/3) - (ml2)/4)

By what logic? Normally you would just add up the MoIs of the simple parts. What is the MoI of AC about B? What is the MoI of BG about B?

For ID I get the answer by doing:

Again, how do you explain the logic behind that?
(Can you see how to use the results of (i) and (ii) and the parallel axis theorem to answer (iii) quickly?)

Here I am using the parallel axis theorem, but why do I subtract the (md2) of the AC rod from the Moment of inertia about D?

I have no idea why you would do such a subtraction, especially since it gives the wrong answer.