More than one equation for a given Trig Graph?

[m3dicat3d]

Hi all.. another Trig question here...

Let's say I'm given a graph of a sinusoidal function and asked to find its equation, but I'm not told whether this is a sine or cosine function and I'm left to determine that myself.

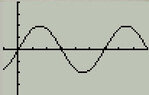
I understand that evaluating where the graph intersects the y-axis is the straight-forward, easiest approach. For instance, take this graph where the y interval is .5 and the x interval is pi/2

View attachment 654

I can say that it's a sine graph easily by sight, but also b/c it intersects the y-axis at y=0. And given the phase shift and no vertical shift, the equation is f(x) = sin [(2/3)x].

BUT, couldn't this also be f(x) = cos [{(2/3)x} - (pi/2)] since sin(x) and cos(x) are separated only by a phase shift of pi/2?

This is meant for my own edification and not to make this kind of exercise more confusing than be. I'm simply interseted if this is in fact mathematically accurate that you could have more than one equation (a sine or a cosine "version") for a given sinusoidal curve.

My calculator returns coincidental curves when I graph both the sine and cosine "versions" of this given graph, but I know my calculator isn't really a mathematician either haha, so I thought I'd ask some real mathematicians instead :)

Thanks

 

[Ackbach]

Note that by the addition of angles identity, that
$$ \cos(2x/3- \pi/2)= \cos(2x/3) \cos( \pi/2)+ \sin(2x/3) \sin( \pi/2)
= \cos(2x/3) \cdot 0+ \sin(2x/3) \cdot 1= \sin(2x/3).$$
So yes, you can definitely have more than one representation of the same graph, as you have seen on your calculator.

 

[m3dicat3d]

Thank You! Thank You! Thank You! Thank You! Thank You!

Excellent answer, and as I am still reviewing my Trig, I hadn't even considered the identity perspective of it... I can't stress enough how much having that perspective helps me even more with this...

Again, Thank you... man this place rocks! (Yes) :D

 

[MarkFL]

As sine and cosine are complementary or co-functions, this just means they are out of phase by $\displaystyle \frac{\pi}{2}$ radians, or 90°.

You may have noticed that a sine curve, if moved 1/4 period to the left, becomes a cosine curve, or conversely, a cosine curve moved 1/4 period to the right becomes a sine curve.

You are doing well to see this, it shows you are trying to understand it on a deeper level rather than just plugging into formulas. Both the sine function and the cosine function, and linear combinations of the two (with equal amplitudes) are called sinusoidal functions.

 

[m3dicat3d]

Thanks MarkFL, I appreciate the encouraging words. I'm studying for my State certification exam to teach HS math here in TX, and I tutor HS students in the meantime. I'm no math genius by far, so when I ask some of my questions I sometimes feel they might be dumb (which no one here has made me feel like I'm glad to say). I'm trying to see those "nuances" in the math in case they might help my students, and again, I appreciate your words, and the full out decency of the community here. It's a great place to learn :)

 

[Ackbach]

Thank You! Thank You! Thank You! Thank You! Thank You!

Excellent answer, and as I am still reviewing my Trig, I hadn't even considered the identity perspective of it... I can't stress enough how much having that perspective helps me even more with this...

Again, Thank you... man this place rocks! (Yes) :D

You're quite welcome! Glad to be of help.