Morin classical mechanics differential equation problem

[member 731016]

Homework Statement

Please see below

Relevant Equations

d^2x/dt^2 = dv/dt = a

I was reading the oscillations chapter which was talking about how to solve linear differential equations. He was talking about how to solve the second order differential below, where a is a constant:

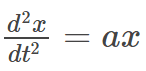
In the textbook, he solved it using the method of substitution i.e guessing the solution. However, how would we solve this differential equation using the method of separation of variables?

I tried solving it using the definition of acceleration, however, I don't think you can do that since v is the derivative of x.

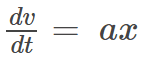
However, if we do use definition of the position,

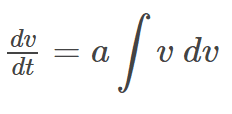
Many thanks!

 

[Orodruin]

You wouldn’t. It is not an ODE of the form $x’ = f(x) g(t)$.

The typical way of solving a linear ODE with fixed coefficients is to make the ansatz $e^{kt}$ and find the allowed values of k.

 

[member 731016]

You wouldn’t. It is not an ODE of the form $x’ = f(x) g(t)$.

The typical way of solving a linear ODE with fixed coefficients is to make the ansatz $e^{kt}$ and find the allowed values of k.

Thank you @Orodruin !

 

[malawi_glenn]

Aren't differential equations of the form $y'' = ky$ a prerequisite for classical mechanics classes these days?

 

[member 731016]

Aren't differential equations of the form $y'' = ky$ a prerequisite for classical mechanics classes these days?

@malawi_glenn I'm a not taking any classical mechanics classes. I'm a year 12 from New Zealand (Still got a year of high school to go).

 

[kuruman]

Aren't differential equations of the form $y'' = ky$ a prerequisite for classical mechanics classes these days?

Not necessarily. Even back in the old days when I took classical mechanics, I saw how to solve $y''-2by'+\omega^2y=0$ in classical mechanics taught by the physics department before I saw it in an ODE course taught by the math department. If you think about it, classical mechanics is, in most places, a fourth semester course after three semesters of intro mechanics, E&M and 20th century physics a.k.a. Modern Physics. Concurrent with these are three semesters of calculus. By the time students are ready to take classical mechanics, an ODE course would at best be a co-requisite, not a prerequisite.

 

[member 731016]

Not necessarily. Even back in the old days when I took classical mechanics, I saw how to solve $y''-2by'+\omega^2y=0$ in classical mechanics taught by the physics department before I saw it in an ODE course taught by the math department. If you think about it, classical mechanics is, in most places, a fourth semester course after three semesters of intro mechanics, E&M and 20th century physics a.k.a. Modern Physics. Concurrent with these are three semesters of calculus. By the time students are ready to take classical mechanics, an ODE course would best be a co-requisite, not a prerequisite.

Thank you @kuruman for the info! To be a physics major in NZ you don't even have to take an ODE course as a requirement, which is kind of surprising compared to what they make US physics majors take.

 

[malawi_glenn]

@malawi_glenn I'm a not taking any classical mechanics classes. I'm a year 12 from New Zealand (Still got a year of high school to go).

We do basic ODE's in swedish high school, year 12.
Just doing morin for fun?

 

[member 731016]

We do basic ODE's in swedish high school, year 12.
Just doing morin for fun?

Interesting @malawi_glenn ! Well, I got an offer to skip to second year university physics next year in NZ if I don't want to go for my finial year of high school (year 13 is what they call it over here). So, I've just being preparing a bit for that. Reading morins for it is probably over preparing for it thought!

Many thanks,
Callum