- #1
Daniel Boy
- 4
- 0
By Lagrange's formalism, the motion equations for double pendulum are:
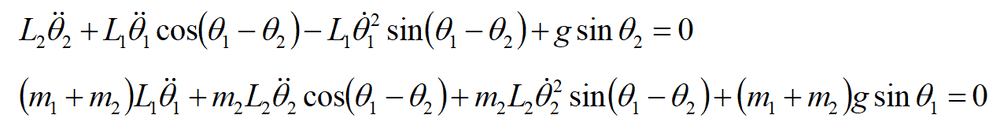
Using Newton's formalism I can't obtain the second equation. Anyone can help?
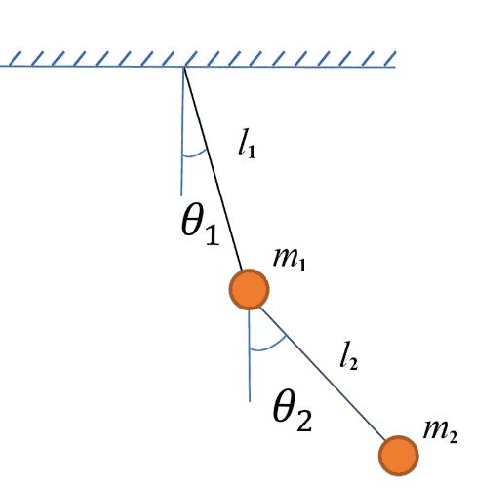
Using Newton's formalism I can't obtain the second equation. Anyone can help?
 ##\qquad## !
##\qquad## !