Motion of a body - conveyor/catapult/trebuchet design

[rmf17]

Hello All,
I posted this same question to the classical physics forum - but I'm reckoning it's more ideally suited for a Mechanical Engineer:

I'm currently working through a scenario in which the following occurs:

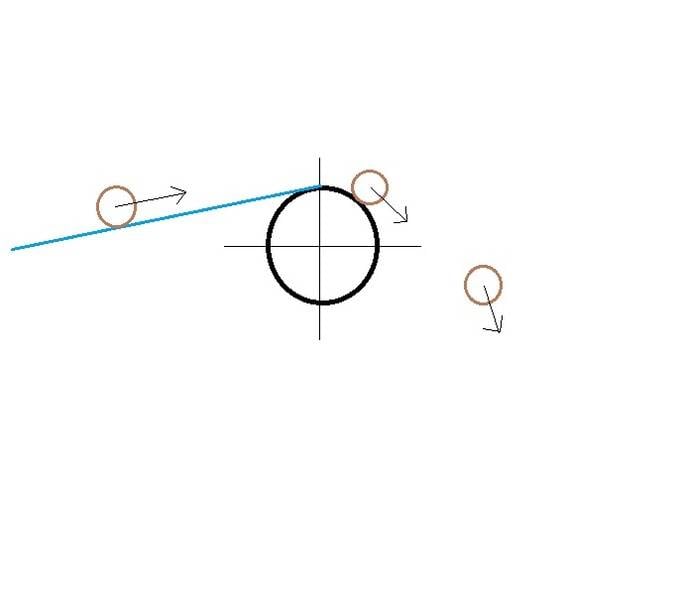
• An object of mass M1 (kg) approaches a rotating wheel at a speed of S1 (m/s) along a belt
• The belt is at an angle Th1 (degrees) to the horizontal axis
• The rotating wheel has a linear velocity equal to S1 (m/s), and a diameter of D1 (m)
• The object of mass M1 (kg) has a centre of mass of distance X1 (m) above the belt surface
• The mass travels around the outer edge of the wheel until such a point as its combined velocity, acceleration and mass components cause it to leave the surface of wheel - this is the tangent or lift point of the object
• The mass then continues to travel under the effect of gravity (assuming no air resistance), proscribing an arc for 3 seconds. After 3 seconds we are no longer interested in its position or characteristics.

I'm creating a spread sheet that for any M1, S1, Th1, D1, X1 the relative location, velocity, acceleration can be found for any moment leading up to the lift point and in the 3 seconds after.
I hope to have the spread sheet plot this trajectory curve - not ideal but I'm limited at work as to what software I can use. I hope to build a VisSim model of it later.

While I have motion equations these are only in affect from the point of lift, this point is highly variable based on the mass, velocity, angel etc.

Can anyone please help me to get the correct relationships and equations in order?

Thanks for helping:)

 

[Navin A S]

</code>This is a very complex problem and it will require a lot of analysis and calculations to solve. It is not something that can be answered in a few simple equations. You will need to start by doing some basic physics calculations in order to determine the forces acting on the object at the lift point. This will involve calculating the centrifugal force, gravitational force, and the friction force between the belt and the wheel. Once you have these values you can use them to calculate the acceleration of the object at the lift point, which will then allow you to calculate the velocity and position of the object after 3 seconds.You will also need to consider the effects of air resistance on the object's motion. For example, if the object is traveling at a high speed, then air resistance will cause the object to slow down over time. You will need to take this into account when calculating the motion of the object.Finally, you may want to consider using numerical simulations to solve the problem. This will give you a more accurate result than using simple equations. There are several software packages available that can be used to simulate the motion of the object, such as MATLAB or COMSOL.Good luck with your project!