Motion of particles close to the Earth

[flyleaf_]

Homework Statement

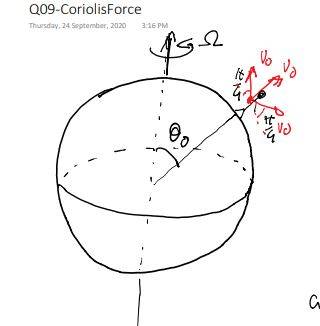
Problem: A spherical body is rotating with angular velocity (=Omega constant) on the z-axis. A person throws 3 balls with initial speeds v0:
1-) First ball to the north with angle pi/4 to the surface
2-) Second ball pi/2 degrees to the surface (right upwards)
3-) Third ball to the south with angle pi/4 to the surface

Find where the balls will land. Assume v<v_escape at any time.

Relevant Equations

v<v_escape at any time;
Radius of the planetary body = a;
Initial latitude = theta_0

I tried to solve the problem in 2 ways, first using lagrangian mechanics and second by putting a rotating reference frame on the initial take-off point.

However I cannot be sure if the equations of motion for the two solutions came out the same.

A-) Equations of motion from Lagrangian Solution:

d/dt(dx/dt) = -G*M_earth*x/((x^2+y^2+z^2)^3/2);
d/dt(dy/dt) = -G*M_earth*y/((x^2+y^2^z^2)^3/2),
d/dt(dz/dt) = -G*M_earth*z/((x^2+y^2+z^2)^3/2);

B-) Equations of motion from the rotating reference frame solution:
d/dt(dx/dt) = 2*omega*(dy/dt*cos(theta)-dz/dt*sin/theta);
d/dt(dy/dt) = -2*omega*dx/dt*cos(theta) - omega^2*a*sin(theta)^2-g;

When I use the equations from Lagrangian, I feel like I omitted something leaving some terms relating the orbital motion out. I am not sure if any of the two solutions are true. After I find the equations of motion, I will use the equations and the initial conditions to numerically solve the problem. Then I will use conservation laws at the problem to choose the best numerical method to solve this problem. However I am stuck at this stage. I would be glad if anyone helped.

 

[mfb]

v<v_escape makes sure it lands again, but there are useful approximations that only work if v<<v_escape. Without these things get complicated.

Solving this analytically in the rotating reference frame will be really messy or even impossible.

The equations of motion in your first approach are simply from Newtonian mechanics. They work, of course. In practice you probably want to use the knowledge that free-fall trajectories are ellipses, and calculate parameters of these ellipses.