Motor Torque to Stabilize Inverted Pendulum

[NeuralNet]

I am trying to stabilize an inverted pendulum with a physical system as follows:

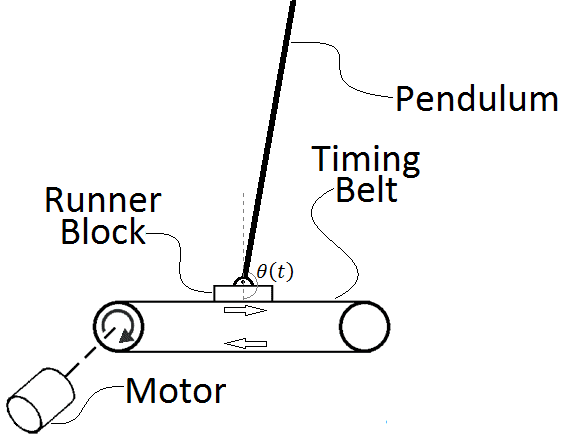
The measured values of the pendlums angle and the cart (runner block) position are sent to a digital controller. The digital controller then outputs a value that is sent to the motor to turn the belt pulley system which in turn moves the cart.

The problem I am having is my equations are such that the value coming out of the controller is the force (in Newtons) that needs to be applied to the cart to move it. I need to convert the force value to the torque value at the motor.

How do I do that?

I am an EE major, and don't know too much about ME stuff. Any help is much appreciated.

 

[NeuralNet]

Here is a more detailed image:

ADC = Analog to Digital Converter
DAC = Digital to Analog Controller
There is an amplifier after the DAC that is not show.

That u(t) value is currently the force (in Newtons) that needs be applied to the cart (not shown in the figure), I need to convert this to the torque value of the motor (as seen in the diagram).

How do I do that?

 

[pukb]

For that , I will need value of coefficient of friction. Assuming angle of contact to be 180 degrees, I can calculate torque = (force - force on lower side) * radius of pulley.

 

[NeuralNet]

We are modelling with coefficient of friction to be negligible.

When you say:
torque = (force - force on lower side) * radius of pulley

What are you referring to when you say 'force on lower side'?

 

[hihiip201]

We are modelling with coefficient of friction to be negligible.

When you say:
torque = (force - force on lower side) * radius of pulley

What are you referring to when you say 'force on lower side'?

isn't the torque just equal to the force require times the radius of the pulley? assuming if you are only operating one of the pulley?