0kelvin
- 50
- 5
I'm studying calculus alone with textbooks. The part about moving the graphs to the right or to the left struck me because they just have a list of rules, properties and make you relate the graph with the corresponding equation. I know what is the rate of change and I thought I could do better than the textbook.
I vectorized this to explain why: f(x - n) moves the parabola to the right.
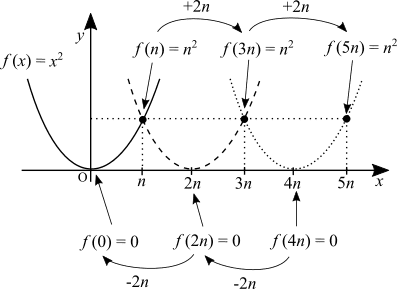
Not satisfied I though. f(x - 2) does remind me of the concept of a composite function. Can I draw something to explain this and relate it to the rate of change?
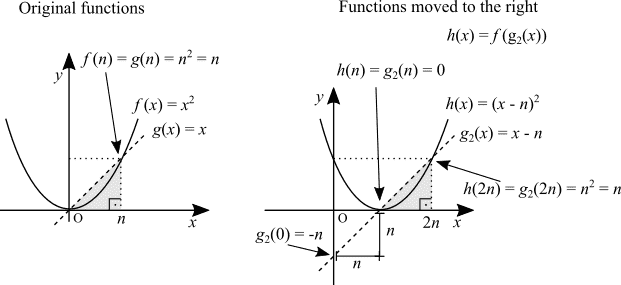
I vectorized this to explain why: f(x - n) moves the parabola to the right.
Not satisfied I though. f(x - 2) does remind me of the concept of a composite function. Can I draw something to explain this and relate it to the rate of change?