MSE estimation with random variables

[ashah99]

Homework Statement

Please see below: finding an MSE estimate for random variables

Relevant Equations

Expectation formula, MSE = E( (S_hat - S)^2 )

Hello all, I am wondering if my approach is correct for the following problem on MSE estimation/linear prediction on a zero-mean random variable. My final answer would be c1 = 1, c2 = 0, and c3 = 1. If my approach is incorrect, I certainly appreciate some guidance on the problem. Thank you.

Problem

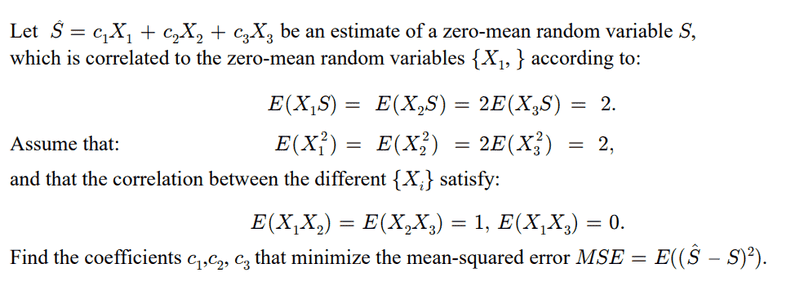
Approach:

 

[andrewkirk]

Yes, the approach is incorrect. When you take expected values, you assume that
$$E\left[ \hat S X_i\right] = E\left[ S X_i\right]$$
But we have no reason to suppose that is correct. $\hat S$ is only an estimate of $S$, not identical to it, and cannot be substituted for it, except in very limited circumstances.

Instead, substitute $\sum c_i X_i$ for $\hat S$ in $E[(\hat S - S)^2]$, then expand to get an expression in expected values of first and second order terms in $X_1, X_2, X_3, S$, with unknowns $c_1,c_2,c_3$. We have been given values for all those terms except $E[S^2]$, which we can ignore, since it it is not multiplied by any of the unknown coefficients. Numerically minimising that expression, I get a solution where two of the coefficients are near 1 and one is near 0. Possibly the optimisation can be solved analytically, but I didn't try.