##\mu##2##e\gamma## probability

[ChrisVer]

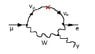
I was doing an exercise with the decay: \mu \rightarrow e \gamma
which violates the lepton number but it is (in principle) allowed due to neutrinos interactions.
The exercise asked to approach the problem with the HUP and find the time interval and "distance" traveled by the intermediate neutrinos, and compare it to the km scale of neutrino oscillations.
L= c \Delta t = \frac{\hbar c}{2 M_W} \sim 10^{-21}~ km
Obviously very small...

I was wondering if anyone knows a way that uses the normal derivation for the probability of this interaction. In particular I am not sure I know how to use the fermion propagator lines for the neutrinos when at some point there is a flavor change.

I think experimentally the Branching ratio has been found to be less that $0.57 \times 10^{-12}$
http://en.wikipedia.org/wiki/Mu_to_E_Gamma

 

[mfb]

Obviously very small...

At the length scale of the weak interaction.
What does the neutrino mixing formula tell you about the probability for this length and an energy you have to choose?

You can safely ignore all factors between .1 and 10. Just the mixing probability makes the decay impossible for all practical purposes.

 

[ChrisVer]

Well first of all the energy of the neutrinos is also needed and \Delta m^2..but I think the L's smallness is enough to make the sins in the probability approximately equal to their arguments.
So the probability should go like P \sim (\Delta m^2)^2 L^2 \sim 10^{-48}

I don't know about the energy...

 

[mfb]

So the probability should go like P \sim (\Delta m^2)^2 L^2 \sim 10^{-48}

That doesn't work in terms of units. The energy is part of the formula.

As higher energies lead to less mixing, using the muon mass is probably a conservative estimate.

 

[ChrisVer]

Or do you mean to set the probability for the transition maximum:
\sin^2 \Big( 1.2 \frac{L}{E} \Delta m^2 \Big)=1?
Then I guess E(GeV) \approx 0.7 L(km) \Delta m^2
I don't know this becomes an extremely small energy and that's why I wouldn't think of it.

 

[ChrisVer]

Ah Ok...then

\sin^2 \Big(1.2 \frac{L(km)}{E(GeV)} \Delta m^2 \Big) \approx \sin^2 \Big( 1.2 \frac{10^{-21}}{0.1} 10^{-3~ \text{to}~ -5}\Big) \approx 10^{-46} ~\text{to}~ 10^{-50}

 

[mfb]

That is in the right range. A few orders of magnitude more or less do not matter, as there is absolutely no way we can find the standard model decay without advanced magic.

 

[ChrisVer]

However I don't know how to express a diagram that looks like this:

 

[mfb]

What do you mean with "express"?
Calculate properly? That takes much more effort, and where is the point? Not even the experts bother calculating this more precise than the order of magnitude (sometimes not even that).

 

[ChrisVer]

Well not calculate if it's so bothersome. Just trying to see how to write the terms in the propagator... (especially for the neutrino transition).

 

[The_Duck]

Well not calculate if it's so bothersome. Just trying to see how to write the terms in the propagator... (especially for the neutrino transition).

Someone should correct me if I'm wrong because I'm not too familiar with this, but I think the neutrino line can be written
\sum_{i=1}^3 U_{\mu,i} \frac{1}{p_\mu \gamma^\mu - m_i} (U_{e,i})^*
where $U$ is the PMNS matrix and $i$ labels the neutrino mass eigenstates.

Note that if all the $m_i$'s are equal, then the overall expression is proportional to $\sum_i U_{\mu,i} (U_{e,i})^*$ which is zero because it is an off-diagonal element of $U U^\dagger= I$. So the amplitude is going to end up proportional to a difference of neutrino masses, or probably a difference of squared masses.

If you expand the above expression as a power series in the masses $m_i$, then I think the first order term is

\frac{1}{p_\mu \gamma^\mu}\left(\sum_{i=1}^3 m_i U_{\mu,i} (U_{e,i})^*\right) \frac{1}{p_\nu \gamma^\nu}

This corresponds to how your diagram is drawn. There is a massless propagator for the electron neutrino, a massless propagator for the muon neutrino, and an insertion of the neutrino mass matrix which produces the $\nu_\mu \to \nu_e$ transition. Now we are treating the neutrino masses as perturbations; they lead to vertices like your red X at which we should insert the central expression in parentheses above.

 

[Hepth]

Actually you can't do that, because each of the vertices with the W boson and the neutrio have a $$P_L$$ projector, so if there's no masses you have

$$\gamma^{\mu} P_L \not p \not p \gamma^{\nu} P_L $$

which is zero, as the P_L ...P_L -> (...) P_R P_L

So the masses are necessary in the propagators too. Basically you have to expand it out to a higher order than what you have.

So not only is it suppressed by the mass insertion, but additionally because of the dirac structure of the currents, only mass-proportinoal terms survive. So this will go like m^2 at the amplitude level.

 

[tg85]

I think the branching ratio, compared with the eνν decay, was calculated as early as 1977 in this paper (eq. 8) by Petcov, downloadable http://ccdb5fs.kek.jp/cgi-bin/img_index?197702078 . It also appears here (eq. 10). Both are from before the actual discovery of neutrino oscillations, but it should be possible to insert current values for the mass-splittings and PMNS-elements.

 

[ChrisVer]

in this paper (eq. 8) by Petcov, downloadable http://ccdb5fs.kek.jp/cgi-bin/img_index?197702078 .

My neck hurts... But I was able to see the formula.

It also appears here (eq. 10).

I don't have access at the moment, I will try it tomorrow.