Multipole expansions, calculating the various moments of point charges

Thread starter milkism
Start date Apr 23, 2023
Tags

Charges Electrostatic Moments Multipole Multipole expansion Point Point charges

Click For Summary

The discussion focuses on the calculation of multipole expansions for point charges, emphasizing the determination of various moments. Participants express satisfaction with the clarity and thoroughness of the solutions provided. There is a consensus that the explanations are well-articulated and effectively motivate the concepts. The overall tone is positive, with contributors appreciating the depth of understanding demonstrated. The conversation reinforces the importance of clear communication in complex physics topics.

Apr 23, 2023

milkism

Homework Statement: Calculate the mono-di and quadrupole moments of the three charges.

Relevant Equations: See solution.

Problem:

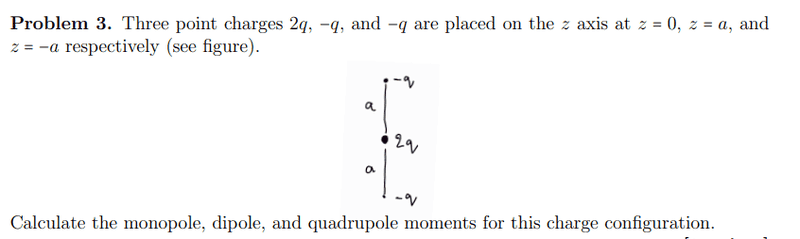
Solution:

This was quite simple, are my solutions correct?

Physics news on Phys.org

Apr 23, 2023

TSny

Science Advisor

Homework Helper

Gold Member

Looks very good to me.

Apr 23, 2023

PhDeezNutz

I love your explanations and motivations. Very thorough.

Thread 'Product of two boosts and then two inverse boosts is rotation matrix'

So is there some elegant way to do this or am I just supposed to follow my nose and sub the Taylor expansions for terms in the two boost matrices under the assumption ##v,w\ll 1##, then do three ugly matrix multiplications and get some horrifying kludge for ##R## and show that the product of ##R## and its transpose is the identity matrix with det(R)=1? Without loss of generality I made ##\mathbf{v}## point along the x-axis and since ##\mathbf{v}\cdot\mathbf{w} = 0## I set ##w_1 = 0## to...

View full post »