Multivariable calculus problem involving partial derivatives along a surface

  • #1
sss1
50
2
Homework Statement
Image
Relevant Equations
NA
I just wanted to know if my solution to part (b) is correct. Here's what I did:
I took the partial derivative with respect to x and y, which gave me
{font:{family:Arial,color:#000000,size:11},aid:null,backgroundColor:#ffffff,id:11,code:$$\\frac{-x}{\\left(x^{2}+y^{2}\\right)^{3/2}},\\,\\frac{-y}{\\left(x^{2}+y^{2}\\right)^{3/2}}$$,type:$$,ts:1695899323324,cs:mLppUJ1pren6kF2+GAN3Fw==,size:{width:192,height:40}}
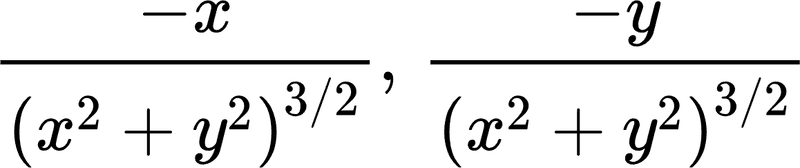respectively.
Then I computed the partial derivatives at (-3,4) which gave me 3/125 for partial derivative wrt x and -4/125 for partial derivative wrt y
Then since directional derivative requires a direction, I just chose an arbitrary one, uhat=(a,b)
since u is a unit vector that means sqrt(a^2+b^2)=1, or a^2+b^2=1.
I then solved for a, which is the plus minus of sqrt(1-b^2).

I just chose to use the positive answer here instead.
So the directional derivative is 3sqrt(1-b^2)/125-4b/125
To maximise this I took the derivative, which is -3b/125sqrt(1-b^2)-4/125
I set it to 0 and solved for b, which gave me -4/5.
So there is a local maximum for the directional derivative at b=-4/5 (I evaluated the second derivative and it was positive).
So that means on both sides of b=-4/5 the directional derivative decreases.
Subsituting b=-0.8 into my formula for a, a=sqrt(1-b^2), gives me a=0.6
So the directional derivative should be a maximum in the direction given by the unit vector (0.6, -0.8, 0) with magnitude 0.6(3/125)-0.8(-4/125) which is 0.04?

Although I didn't try the negative answer for a, a=-sqrt(1-b^2), I believe that this will yield a smaller answer because if a is negative, then a negative number times a positive number (3/125) will decrease the answer overall? Is my logic correct?
Screen Shot 2023-09-28 at 20.43.41.png
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
The gradient of a function evaluated at a point tells you the direction in which the function increases most rapidly at that point. This would give you the answer more quickly.
 
  • Like
Likes DeBangis21
  • #3
PeroK said:
The gradient of a function evaluated at a point tells you the direction in which the function increases most rapidly at that point. This would give you the answer more quickly.
Can you explain how to do it using this method?
 
  • #4
sss1 said:
Can you explain how to do it using this method?
You could have just plugged ##x = -3, y = 4## into the derivative you calculated.
 
  • #5
PeroK said:
You could have just plugged ##x = -3, y = 4## into the derivative you calculated.
derivative as in df/dt?
 
  • Sad
Likes PeroK
  • #6
sss1 said:
derivative as in df/dt?
Look up what gradient means for a multi-variable function.
 
  • #7
PeroK said:
Look up what gradient means for a multi-variable function.
f_x(x,y)i+f_y(x,y)j? I plugged in (-3,4) and it gave me (3/125, -4/125)
 
  • #8
sss1 said:
f_x(x,y)i+f_y(x,y)j? I plugged in (-3,4) and it gave me (3/125, -4/125)
But isn't that the gradient at (-3,4)? How is that the direction f increases most rapidly?
 

FAQ: Multivariable calculus problem involving partial derivatives along a surface

What is a partial derivative in the context of multivariable calculus?

A partial derivative is a derivative where the function depends on multiple variables, and we take the derivative with respect to one of those variables while keeping the others constant. It measures how the function changes as one specific variable changes, providing insight into the behavior of the function in a multi-dimensional space.

How do you find the partial derivatives of a function defined on a surface?

To find the partial derivatives of a function defined on a surface, you first express the function in terms of the variables that describe the surface. Then, you take the derivative of the function with respect to each of these variables, treating all other variables as constants. This process yields the partial derivatives along the surface.

What is the geometric interpretation of partial derivatives on a surface?

The geometric interpretation of partial derivatives on a surface is that they represent the slope or rate of change of the function in the direction of the corresponding variable. For example, if you have a surface defined by z = f(x, y), the partial derivative with respect to x (∂f/∂x) represents the slope of the surface in the x-direction, while the partial derivative with respect to y (∂f/∂y) represents the slope in the y-direction.

How do you apply the chain rule to partial derivatives on a surface?

The chain rule for partial derivatives is used when the variables are functions of other variables. If you have a function z = f(x, y) and x and y are themselves functions of other variables, say u and v, then the chain rule helps you find the partial derivatives of z with respect to u and v. The chain rule states that ∂z/∂u = (∂z/∂x)(∂x/∂u) + (∂z/∂y)(∂y/∂u) and similarly for ∂z/∂v.

What are some common applications of partial derivatives on surfaces?

Partial derivatives on surfaces have numerous applications in various fields. In physics, they are used to describe the behavior of physical systems, such as heat distribution and fluid flow. In economics, they help in understanding how changes in one variable affect others in a multi-variable system. In engineering, partial derivatives are crucial for optimizing design parameters and analyzing stress and strain on surfaces.

Similar threads

Existence of directional derivative
Replies
4
Views
986
Determining domain for C^1 function
Replies
4
Views
756
Find f(x,y) given partial derivative and initial condition
Replies
6
Views
1K
"Trick" for a specific potential function defined with an integral
Replies
10
Views
2K
Unit Normal to a level surface
Replies
2
Views
2K
Calculate this Integral around the Circular Path using Green's Theorem
Replies
3
Views
1K
Problem 1-23 and 1-24 from Spivak's Calculus on Manifolds
Replies
6
Views
1K
IVP problem using Laplace transform and partial fractions
Replies
1
Views
662
Problem about existence of partial derivatives at a point
Replies
3
Views
3K
I Differentiability of a Multivariable function
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top