Multivariable optimization problem

[Doc]

TL;DR Summary

Stress minimization in design of spring clip

Hi all,

(Please move to general or mechanical engineering sub-forum if more appropriate over there. I put this here as it is essentially a mathematics problem.)

Broken into sections:
- problem categorization (what type of problem I think I have),
- the question,
- specifics (description of the design task and all variables),
- solution attempt.

Problem categorization

I have a design task that I believe to be a multivariable constrained optimization problem.

Question

I have a stress induced in a piece of glass by a spring clip σG(D,w), how do I minimize this stress in the context of multivariable optimization? Or is there a more appropriate way to solve this problem?

Specifics

I need to design a spring clip (three identical clips will be used) that will retain a piece of glass in a mount, Figure 1.

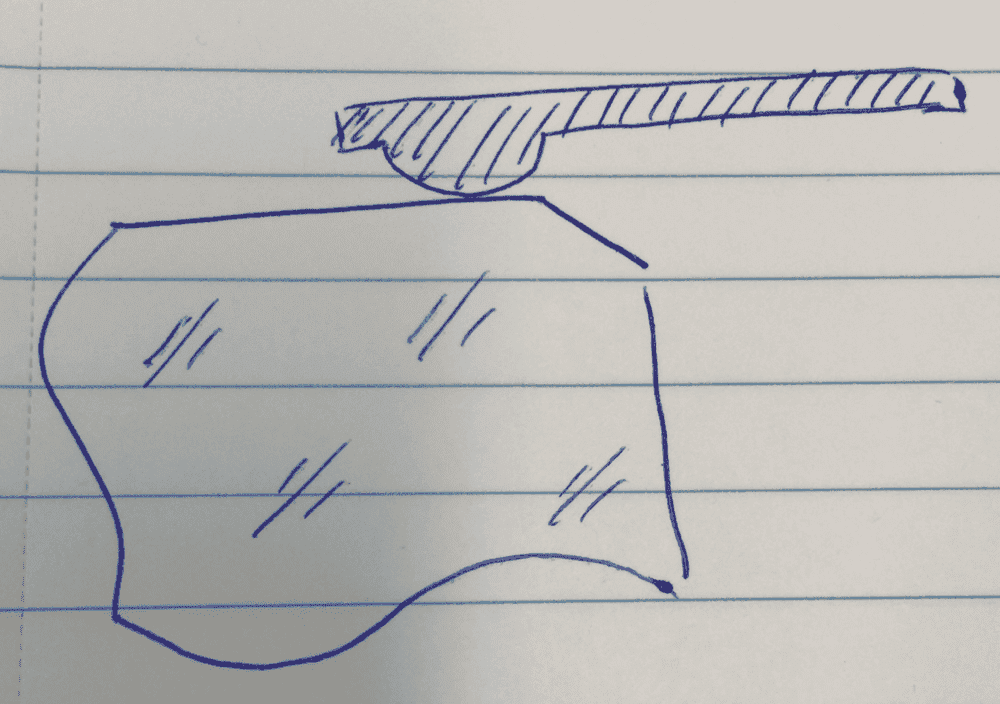
Figure 1, spring clip shown retaining cut-away section of glass.

The clip needs to retain the glass with a set preload, F. The clip preload will induce a compressive stress in the glass, σg, and this should be minimised so as not not damage the glass. Figure 2 shows a diagram of the spring clip with its associated dimensions, ignore t and L for now.

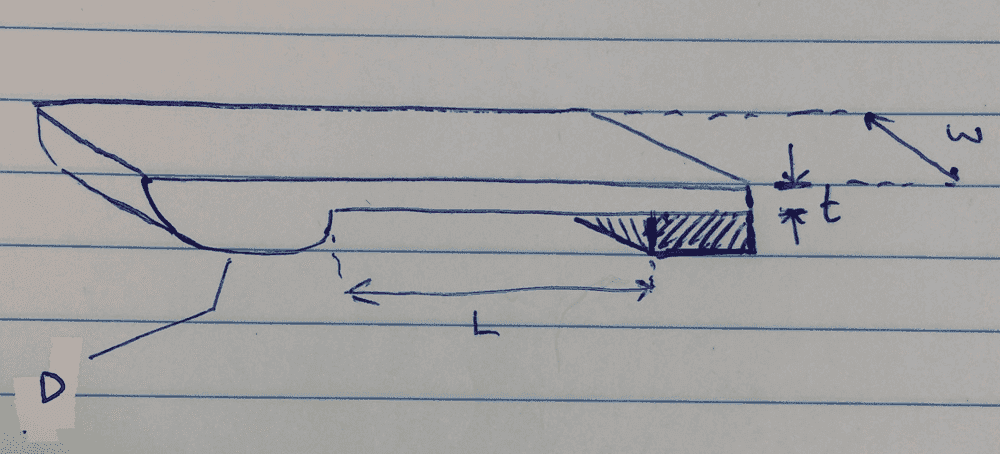
Figure 2.

The stress induced in the glass is given by:

$$\sigma_G = 0.798 \sqrt { \frac {K_1 \frac {F} {w} } {K_2} }$$

Where w is the width of the spring clip and:

$$K_1 = \frac {1} {D}$$

And:

$$K_2 = \left[ \frac {(1- \nu^2_G)} {E_G} \right] + \left[ \frac {(1- \nu^2_M)} {E_M} \right]$$

ν is the material Poissons ratio and E is the material Young's modulus. The subscripts G and M refer to glass and metal, respectively.

Therefore the stress in the glass, σg, is a function of the diameter, D, of the rounded end of the clip and the width of the clip: the rest of the components may be considered constants. So I have:

$$\sigma_G (D,w)$$

Solution attempt

The procedure, as I understand it, is to:
1. reduce the equation or quantity that I want to optimize (minimize in this case) and reduce it down to a single variable,
2. differentiate,
3. set equal to 0,
4. solve for the variable.

In order to achieve step 1 I will simply say that, for practicality in using the clip after manufacture, D > w. To keep things simple I'll say that D = 2w.
Recall the equation for stress:

$$\sigma_G = 0.798 \sqrt { \frac { \frac {1} {D} \frac {F} {w} } {K_2} }$$

I can then substitute D and rewrite the stress equation:

$$\sigma_G = 0.798 \sqrt { \frac { \frac {1} {2w} \frac {F} {w} } {K_2} }$$

Combining terms and simplifying gives:

$$\sigma_G = 0.798 \sqrt { { \frac {F} {2w^2 K_2} } }$$

Taking the constants out of the root gives:

$$\sigma_G = 0.798 \sqrt{ \frac {F} {2w^2} } (w^-1)$$

Taking the derivative gives:

$$\sigma_G = -0.798 \sqrt{ \frac {F} {2w^2} } (w^-2)$$

I got to here and then started getting from what I could tell to be nonsensical answers.

Would be much appreciated if somebody could let me know where I'm going wrong. Apologies, it's been sometime since I last used this stuff.

Regards,
Doc

 

[pbuk]

Why do you think that there is a particular value of $w$ that will minimise the stress, rather than the stress simply decreasing as $w$ is made larger?

It is also not clear from your diagram how the glass is held in place in all 3 dimensions, and whether the clips act on the edges or a face of the glass.

 

[Doc]

Why do you think that there is a particular value of $w$ that will minimise the stress, rather than the stress simply decreasing as $w$ is made larger?

The stress will decrease as either w or d, or both are made larger: that's correct.

It is also not clear from your diagram how the glass is held in place in all 3 dimensions, and whether the clips act on the edges or a face of the glass.

Three clips are equispaced around the glass, and the rounded part of the clips presses against the face of the glass.

There's actually a second stress, that I left out on purpose, that needs to be minimised: σM, the stress induced in the clip itself, where the subscript M denotes metal. I left it out of the original post because I thought that I could apply whatever suggested method/corrections users posted in reply to σG, to that second stress.

To state the problem fully, I have a need to minimize both σG and σM. The stress in the clip is:

$$\sigma_M = \frac {My} {I}$$

Where M is the internal moment induced in the spring clip (treated as a cantilevered prismatic beam, Figure 3), y is the distance from the cross-section neutral axis to the outmost fibre of the beam, and I is the cross-section moment of inertia.

Figure 3. Applied force, F, at free end. Section z-z shows the beam cross-section. Width is w, and thickness is t.

The stress can also be written as:

$$\sigma_M = \frac {(Fl)y} { \frac {1} {12}wt^3 }$$

You can see now that w is a variable in both stresses. Basically I want something like the following:

$$\begin{align} \sigma_G = 0.798 \sqrt{\frac{\frac{1}{D} \frac{F} {w}} {K_2}}&\leq (0.2) \sigma_G,damage \\ \sigma_M = \frac {(Fl)y} { \frac {1} {12}wt^3 }&\leq (SF) \sigma_M,yield \end{align}$$

Where SF is some factor of safety.

I'd like to specify ranges for some of the parameters, for example: 10mm to 25mm for L etc.

My original approach was to set σG as 20% of the damage stress (as I've written above), set D at 50mm so it was easily machined and solve for w. Then I'd use that value of w to aid in finding the dimensions of the clip. It feels a bit, guessy, doing it this way.

Another thought is that optimization may be more applicable to determining σM than σG? D and w in the original post aren't really coupled with each other in the same way that the cross-section dimensions are coupled together to specify the moment of inertia in σM.

Any guidance here is very much appreciated.

 

[pbuk]

The stress will decrease as either w or d, or both are made larger: that's correct.

So in order to minimise stress you simply need to make w (and/or d, but you have already fixed d with respect to w) as large as possible. This will have other consequences, for instance as the clips get larger they will obscure more of the object behind the glass, but your objective function does not take this into account (and I don't think it would be possible to create an objective function that does in any meaningful way).

Three clips are equispaced around the glass, and the rounded part of the clips presses against the face of the glass.

Is the glass vertical? If so, what constrains it from slipping down? What forces (including due to vibration) is the assembly subject to? Why are there 3 clips? What are the safety factors involved (is this a thin slip covering a horizontal specimen in a static display cabinet or plate glass protecting a full height display in a movable partition)?

There's actually a second stress, that I left out on purpose, that needs to be minimised: σM, the stress induced in the clip itself, where the subscript M denotes metal. I left it out of the original post because I thought that I could apply whatever suggested method/corrections users posted in reply to σG, to that second stress.

That stress will also be minimised by making the clip as big as possible.

Any guidance here is very much appreciated.

Search for mirror clip and order some off the shelf; you will note that these generally work by constraining the edge of the glass rather than pressing on the face which means that the forces you are concerned about are not material. And yes, this post does belong in engineering (or DIY).

 

[Doc]

So in order to minimise stress you simply need to make w (and/or d, but you have already fixed d with respect to w) as large as possible. This will have other consequences, for instance as the clips get larger they will obscure more of the object behind the glass, but your objective function does not take this into account (and I don't think it would be possible to create an objective function that does in any meaningful way).

The clip size has a limit due to a clear aperture requirement.

Is the glass vertical? If so, what constrains it from slipping down? What forces (including due to vibration) is the assembly subject to? Why are there 3 clips? What are the safety factors involved (is this a thin slip covering a horizontal specimen in a static display cabinet or plate glass protecting a full height display in a movable partition)?

I appreciate the thought here, but this has been covered in specification of the preload force which I have not covered here.

That stress will also be minimised by making the clip as big as possible.

Yes, but there is a clear aperture requirement meaning that the clips have a size limit.

Search for mirror clip and order some off the shelf; you will note that these generally work by constraining the edge of the glass rather than pressing on the face which means that the forces you are concerned about are not material.

No, these need to be custom. An edge constraint is not practical in this application.

And yes, this post does belong in engineering (or DIY).

I'm not after engineering advice, although I appreciate your input. I was hoping to get some feedback/guidance specifically on the potential for multi-variable optimization: which is why I posted the topic in this sub-forum.

 

[pbuk]

The clip size has a limit due to a clear aperture requirement.
...
Yes, but there is a clear aperture requirement meaning that the clips have a size limit.

In that case both stresses can be minimised by making the clips as large as possible within the limit. This can be seen intuitively and is also confirmed by the fact that the first derivative of the objective functions are always negative.

 

[Doc]

In that case both stresses can be minimised by making the clips as large as possible within the limit. This can be seen intuitively and is also confirmed by the fact that the first derivative of the objective functions are always negative.

I've already decided to make the clips as big as I am able to. This was more of a parallel exercise to learn about the process of optimization, something I will likely be able to apply to other engineering tasks down the road. I thought that optimization may be a way to solve this as I wanted to constrain some of the geometric parameters of the clips to make machining and usage more practical. If you think that this is a bad example for a mathematical approach such as this, that is also a helpful answer.