Mutual inductance of a coil inside a solenoid

[Amaelle]

Good day , i have an issue with the derivation of the mutual inductance of coil inside solenoid formula

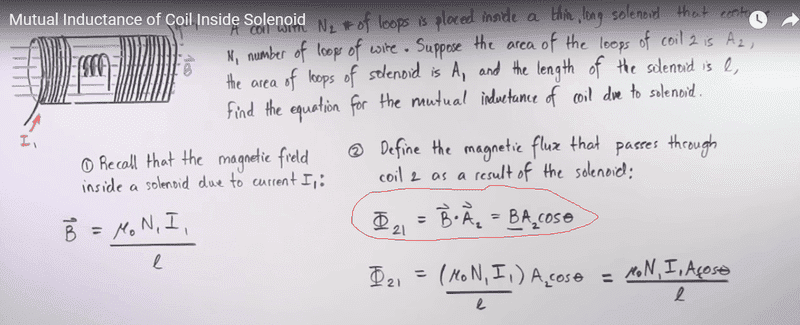
I1 is an alternating current which means that B is varying, and we know that the Flux 21 is equal to the integral of the dot product of B and A2 but as B is varying we CAN NOT take it out of the integral and use the form used in the pic (the formula encercled in red).
Maybe there is something missing in my logic and any help would be highly appreciated, thanks!

 

[TSny]

You can take B out of the integral as long as B doesn’t vary with position.

 

[Amaelle]

thank you for your prompt answer, but I still have difficulty to grasp this point, isn t B varying with time?? because the current is alternating? thanks!

 

[TSny]

Yes, B varies with time. So the flux varies with time. But the flux at any particular instant of time is a spatial integral of B over the surface A₂. At any particular time, B is uniform over the A₂.

 

[Amaelle]

Thanks a million ! you nail it !