annamal
- 393
- 33
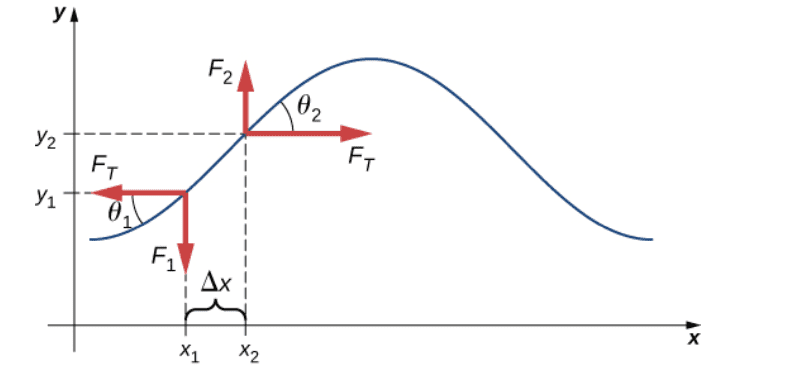
My textbook is deriving wave speed on a string under tension with confusing thetas. It assumes ##\tan \theta_1 = \frac{-F_1}{F_T}## and ##\tan \theta_2 = \frac{F_2}{F_T}## which confuses me. I know for sure theta is the angle due to the position of y and x, ##\tan \theta = \frac{y}{x}##, but I am confused how you can assume that theta is the angle between the forces. Attached is an image of a graph of the y position vs x position of a wave.