- #1
Natural Log Limits: Understanding the Use of L'Hôpital's Rule
In summary, the conversation was about a limit problem involving the use of natural logarithms. The person was confused about how the last step was achieved and asked for clarification. The expert explains that the use of logarithm rules and algebraic manipulation can make solving limits easier and also mentions the use of L'Hôpital's rule.
- #2
lanedance
Homework Helper
- 3,304
- 2
pics always take a while to clear, you;re better writing it up if you can
- #3
bobber205
- 26
- 0
Didn't realize that. Sorry. :)
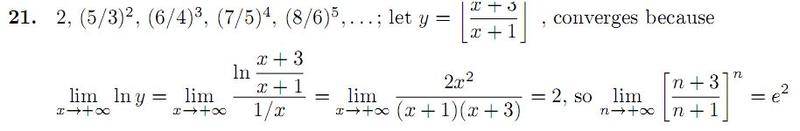
- #4
slider142
- 1,017
- 72
bobber205 said:Didn't realize that. Sorry. :)
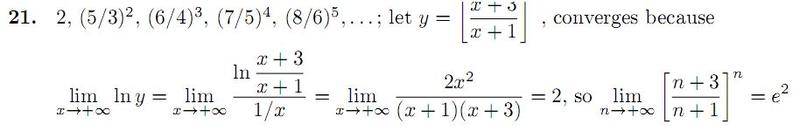
which equality in particular are you having a problem with? Or is it the introduction of the natural logarithm on the left-hand side?
- #5
bobber205
- 26
- 0
I am having trouble with why he choose to let y what it does and how we went on from there.
How did he get
ln ((x+3)(x+1)/(1/x))
How did he get
ln ((x+3)(x+1)/(1/x))
- #6
slider142
- 1,017
- 72
bobber205 said:
This makes each term in the sequence y(x). It is also trivial that y(x) = eln(y(x)), which, in this case, is easier to study. He made use of the logarithm rule: ln(ax) = xln(a), and algebra: x = 1/(1/x), provided x is not 0.
Many limits are easily solved if you can find a clever rewriting of the algebraic expression like this.
- #7
bobber205
- 26
- 0
How did he arrive at the 2x^2 / (x+3)(x+1) step? Is there something I'm missing he did when he took the limit to infinity?
- #8
slider142
- 1,017
- 72
bobber205 said:
The second limit gives us the indeterminate form 0/0, which makes it valid to use L'Hôpital's rule. This was the point of writing x as 1/(1/x).
FAQ: Natural Log Limits: Understanding the Use of L'Hôpital's Rule
What is a natural logarithm?
A natural logarithm is a mathematical function that is the inverse of the exponential function. It is used to solve equations involving exponential growth or decay.
How do you calculate the natural logarithm of a number?
The natural logarithm of a number can be calculated by using a calculator or by using the formula ln(x), where x is the number you want to find the logarithm of.
What is the difference between a natural logarithm and a common logarithm?
The main difference between a natural logarithm and a common logarithm is the base. A natural logarithm has a base of e (approximately 2.718), while a common logarithm has a base of 10.
How are natural logs with limits used in science?
Natural logs with limits are used in science to model and analyze various natural phenomena, such as population growth, radioactive decay, and chemical reactions. They help scientists understand and predict the behavior of these systems.
Can natural logs with limits be negative?
Yes, natural logs with limits can be negative. However, the natural log of a negative number is undefined, as there is no real number that when raised to the power of e will give a negative number.