MasterOgon
- 6
- 21
- TL;DR Summary
- Is it possible to solve the Navier-Stokes equation in a triangular coordinate system and wouldn't this be more accurate?
The Navier-Stokes equation is solved in a vector grid in a Cartesian coordinate system. That is, rectangular. But does a rectangular mesh relate to what happens in a gas or liquid, and is it better to use a triangular mesh?
Undoubtedly, it is incredibly difficult to take into account all the factors even in a triangular or tetrider coordinate system, which is difficult even for visual perception. And in its direct form such a solution is impossible. But it is precisely this system that allows the logical formation of figures that we can see in water - a ring vortex or torus, similar to a figure eight (infinity) and a hexagon, similar to a snowflake or polar vortexes of gas giants.
Let's imagine a homogeneous medium that consists of individual particles. The only possible position of the particles relative to each other, at which absolute homogeneity is achieved, is a tetrider, or for simplicity, a triangular lattice in one plane, at the intersections of which the particles are located. Thus, all distances between particles are the same. Particles interact with each other by being attracted at a distance and repelled upon collision, which is caused by the forces of molecular attraction and repulsion.
Now suppose one particle received an impulse and moved from its place in the direction of the other two. If we considered particles as billiard balls, then we could assume that the momentum would be divided into two. But in this case we have forces of molecular attraction and repulsion, which allow us to regard further interaction as a chain reaction similar to the domino principle, where momentum is transmitted indefinitely due to the force of gravity. Having logically followed the trajectory of the particles, we will see that the impulse in a circle on both sides, forming a figure eight, returned to the first part, which caused the action, which will lead to an endless repetition of the process. It is precisely this mechanism that underlies the ring vortex, which under ideal conditions, according to viscous friction, can exist endlessly dissipating its energy.
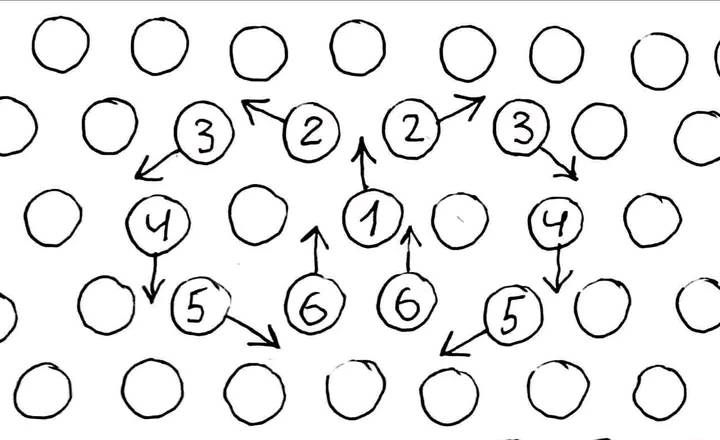
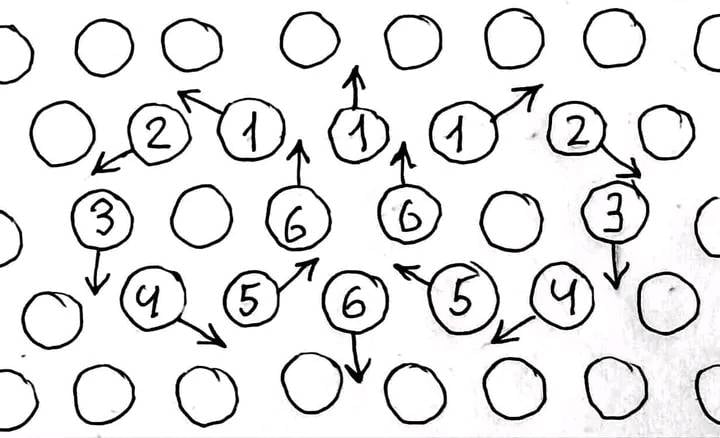


Undoubtedly, it is incredibly difficult to take into account all the factors even in a triangular or tetrider coordinate system, which is difficult even for visual perception. And in its direct form such a solution is impossible. But it is precisely this system that allows the logical formation of figures that we can see in water - a ring vortex or torus, similar to a figure eight (infinity) and a hexagon, similar to a snowflake or polar vortexes of gas giants.
Let's imagine a homogeneous medium that consists of individual particles. The only possible position of the particles relative to each other, at which absolute homogeneity is achieved, is a tetrider, or for simplicity, a triangular lattice in one plane, at the intersections of which the particles are located. Thus, all distances between particles are the same. Particles interact with each other by being attracted at a distance and repelled upon collision, which is caused by the forces of molecular attraction and repulsion.
Now suppose one particle received an impulse and moved from its place in the direction of the other two. If we considered particles as billiard balls, then we could assume that the momentum would be divided into two. But in this case we have forces of molecular attraction and repulsion, which allow us to regard further interaction as a chain reaction similar to the domino principle, where momentum is transmitted indefinitely due to the force of gravity. Having logically followed the trajectory of the particles, we will see that the impulse in a circle on both sides, forming a figure eight, returned to the first part, which caused the action, which will lead to an endless repetition of the process. It is precisely this mechanism that underlies the ring vortex, which under ideal conditions, according to viscous friction, can exist endlessly dissipating its energy.