- #1
unscientific
- 1,728
- 13
For a wavefunction at the Brillouin boundary we have:
\langle k|H|k\rangle = \epsilon_0 (\vec k)
\langle k'|H|k'\rangle = \epsilon_0 (\vec k+\vec G)
\langle k'|H|k\rangle = V_G = \frac{1}{L^3} \int e^{i(\vec k - \vec k') \cdot \vec r} V(r) d\vec r
\langle k|H|k'\rangle = V_G^*
Using degenerate perturbation theory, we diagonalize the hamiltonian and find the eigenvalues (energies) to be:
E_{\pm} = \epsilon_0 (\vec k) \pm |V_g|
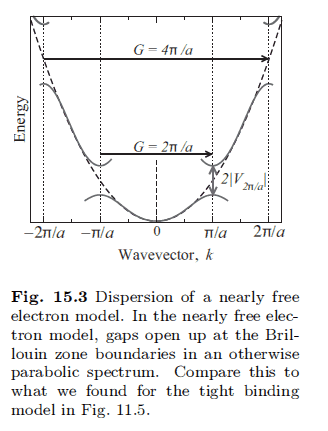
This would mean that for every ##k## right on the boundary we have a bandgap of ##2|V_G|##.Since ## V_G = \frac{1}{L^3} \int e^{i(\vec k - \vec k') \cdot \vec r} V(r) d\vec r##, shouldn't its magnitude be fixed at ##2|V_G##? However, in my notes for a periodic perturbation ##V_G = \tilde V cos(\frac{2n\pi}{a})## the gaps are increasing with ##k## (The bandgap at ##k=\frac{2\pi}{a}## seems to be twice as big as the bandgap at ##k=\frac{\pi}{a}##.
\langle k|H|k\rangle = \epsilon_0 (\vec k)
\langle k'|H|k'\rangle = \epsilon_0 (\vec k+\vec G)
\langle k'|H|k\rangle = V_G = \frac{1}{L^3} \int e^{i(\vec k - \vec k') \cdot \vec r} V(r) d\vec r
\langle k|H|k'\rangle = V_G^*
Using degenerate perturbation theory, we diagonalize the hamiltonian and find the eigenvalues (energies) to be:
E_{\pm} = \epsilon_0 (\vec k) \pm |V_g|
This would mean that for every ##k## right on the boundary we have a bandgap of ##2|V_G|##.Since ## V_G = \frac{1}{L^3} \int e^{i(\vec k - \vec k') \cdot \vec r} V(r) d\vec r##, shouldn't its magnitude be fixed at ##2|V_G##? However, in my notes for a periodic perturbation ##V_G = \tilde V cos(\frac{2n\pi}{a})## the gaps are increasing with ##k## (The bandgap at ##k=\frac{2\pi}{a}## seems to be twice as big as the bandgap at ##k=\frac{\pi}{a}##.