Need explanations about phasor diagram

[MissP.25_5]

How do we know that the phase of I1 is faster than I0? And how do we know that I3 is faster than I2?
How do we know that I2 is the slowest of them all??

 

[gneill]

How do we know that the phase of I1 is faster than I0? And how do we know that I3 is faster than I2?
How do we know that I2 is the slowest of them all??

Okay, a slight misconception there. All of the phasors are assumed to rotate at the same rate. This is tied to the frequency, ω, associated with the driving current.

I think what you are trying to get at is the relative phases of the phasors. Conventionally, for a right-handed coordinate system angles increase from the reference angle in a counterclockwise direction.

 

[MissP.25_5]

Okay, a slight misconception there. All of the phasors are assumed to rotate at the same rate. This is tied to the frequency, ω, associated with the driving current.

I think what you are trying to get at is the relative phases of the phasors. Conventionally, for a right-handed coordinate system angles increase from the reference angle in a counterclockwise direction.

So, it doesn't matter if I3 and I2 switch places?

 

[gneill]

So, it doesn't matter if I3 and I2 switch places?

In the diagram I3 is 90° ahead of I2. If they switched places then I2 would be 90° ahead of I3.

 

[MissP.25_5]

In the diagram I3 is 90° ahead of I2. If they switched places then I2 would be 90° ahead of I3.

How do I know that I3 is ahead of I2?

 

[gneill]

How do I know that I3 is ahead of I2?

It is counterclockwise from I2. (You look for the smaller of the angles between the two, since by convention phases are taken to lie between -180° and +180°).

 

[MissP.25_5]

It is counterclockwise from I2. (You look for the smaller of the angles between the two, since by convention phases are taken to lie between -180° and +180°).

I still don't get it :( Why is I3 counterclockwise from I2? Does the circuit diagram indicate anything about the direction?

 

[gneill]

I still don't get it :( Why is I3 counterclockwise from I2? Does the circuit diagram indicate anything about the direction?

I am going by the provided phasor diagram. Presumably the phasors were determined by an analysis of the circuit.

EDIT: If you consider I2 and I3 in the circuit diagram they are currents through parallel components. That means they share the same potential difference. What do you know about the current phase (with respect to the potential) for those components?

 

[MissP.25_5]

I am going by the provided phasor diagram. Presumably the phasors were determined by an analysis of the circuit.

EDIT: If you consider I2 and I3 in the circuit diagram they are currents through parallel components. That means they share the same potential difference. What do you know about the current phase (with respect to the potential) for those components?

Oh, you mean I3 in the diagram is above I2, so that's why I3 is ahead of I2 in the phasor diagram?

 

[gneill]

Oh, you mean I3 in the diagram is above I2, so that's why I3 is ahead of I2 in the phasor diagram?

Consider the two phasors p1 and p2 in the following diagram:

The smaller angle between the two is $\phi$, so that is the phase difference. p2 is ahead of p1 by phase angle $\phi$, going counterclockwise (positive direction) from p1 to p2. You could also say that p1 lags p2 by phase angle $\phi$.

 

[MissP.25_5]

Consider the two phasors p1 and p2 in the following diagram:

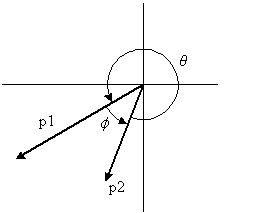
The smaller angle between the two is $\phi$, so that is the phase difference. p2 is ahead of p1 by phase angle $\phi$, going counterclockwise (positive direction) from p1 to p2. You could also say that p1 lags p2 by phase angle $\phi$.

Yes, I got that but what I don't understand is why p2 is ahead of p1?Why not the other way round?
By they way, in the picture I attached, the phasor diagram is the answer. The problem is to find draw the phasor diagram for the circuit (the second picture). But I posted both the problem and answer because I don't understand the answer. I don't know why I2 is ahead of I3. Imagine that the answer isn't there.

 

[gneill]

Yes, I got that but what I don't understand is why p2 is ahead of p1?Why not the other way round?

p2 is ahead of p1 because it lies COUNTERCLOCKWISE to p1, moving through the smaller angle between them.

A phasor diagram takes the rotating vectors of the time domain and 'removes' (or ignores) the time dependent component (that would be the $e^{ωt}$ bits). As a result the phasor diagram is a static depiction of the relationships between voltages and currents in a circuit. If the excised bits were left in, you'd need an animated display to depict all the vectors rotating COUNTERCLOCKWISE at a constant rate ω. Phasors COUNTERCLOCKWISE of a given phasor are leading in phase. Those that are CLOCKWISE are lagging.

By they way, in the picture I attached, the phasor diagram is the answer. The problem is to find draw the phasor diagram for the circuit (the second picture). But I posted both the problem and answer because I don't understand the answer. I don't know why I2 is ahead of I3. Imagine that the answer isn't there.

I3 is ahead because the components carrying the currents share the same potential difference and current LEADS potential by $\pi/2$ radians for a capacitor, but is in step with potential for a resistor. So the capacitor current (I3) must LEAD that of the parallel resistor by $\pi/2$ radians.

 

[MissP.25_5]

I3 is ahead because the components carrying the currents share the same potential difference and current LEADS potential by $\pi/2$ radians for a capacitor, but is in step with potential for a resistor. So the capacitor current (I3) must LEAD that of the parallel resistor by $\pi/2$ radians.

Aaaaa...I got it now! This explains a lot. Thank you so much for your patience.

 

[MissP.25_5]

p2 is ahead of p1 because it lies COUNTERCLOCKWISE to p1, moving through the smaller angle between them.

A phasor diagram takes the rotating vectors of the time domain and 'removes' (or ignores) the time dependent component (that would be the $e^{ωt}$ bits). As a result the phasor diagram is a static depiction of the relationships between voltages and currents in a circuit. If the excised bits were left in, you'd need an animated display to depict all the vectors rotating COUNTERCLOCKWISE at a constant rate ω. Phasors COUNTERCLOCKWISE of a given phasor are leading in phase. Those that are CLOCKWISE are lagging.

I3 is ahead because the components carrying the currents share the same potential difference and current LEADS potential by $\pi/2$ radians for a capacitor, but is in step with potential for a resistor. So the capacitor current (I3) must LEAD that of the parallel resistor by $\pi/2$ radians.

Ok, just to make sure that I really get it, can you check this for me please? Am I drawing it right? Sorry, the picture is a bit blurry but you can still see it, I bet.

 

[gneill]

Ok, just to make sure that I really get it, can you check this for me please? Am I drawing it right? Sorry, the picture is a bit blurry but you can still see it, I bet.

I see that you've taken the current I as the phase reference. Since R1 and L are in series and carry current I, then your diagram is correct for them: V1 is in phase with I, and V2 is advanced by 90° as you've drawn.

V3 and E are a bit trickier. While R2 and C are in parallel as in the previous case in this thread, this time you're looking for voltage phases not current phases, and since the components are in parallel, they must both have the same voltage and phase. While the capacitor current will lead that of R2 by 90°, that doesn't tell us the specific relationship to I, so it doesn't tell us the specific relationship of the voltage phases with respect to I, either. E is also going to have some phase with respect to I, determined by the sum of the other voltage phasors. So the phases for V3 and E are going to depend upon particular component values.

V3's phase will lie somewhere between 0 and -90 degrees with respect to I, but I don't see it being exactly -90°. Depending upon the particular values of the components, and thus where V3 ends up, E could lie above or below I in terms of phase.

I don't suppose you're given component values for this problem?

 

[MissP.25_5]

I see that you've taken the current I as the phase reference. Since R1 and L are in series and carry current I, then your diagram is correct for them: V1 is in phase with I, and V2 is advanced by 90° as you've drawn.

V3 and E are a bit trickier. While R2 and C are in parallel as in the previous case in this thread, this time you're looking for voltage phases not current phases, and since the components are in parallel, they must both have the same voltage and phase. While the capacitor current will lead that of R2 by 90°, that doesn't tell us the specific relationship to I, so it doesn't tell us the specific relationship of the voltage phases with respect to I, either. E is also going to have some phase with respect to I, determined by the sum of the other voltage phasors. So the phases for V3 and E are going to depend upon particular component values.

V3's phase will lie somewhere between 0 and -90 degrees with respect to I, but I don't see it being exactly -90°. Depending upon the particular values of the components, and thus where V3 ends up, E could lie above or below I in terms of phase.

I don't suppose you're given component values for this problem?

Well, here's the actual question.
In the diagram’s circuit, the effective value of E is 100 [V], angular frequency is 10[rad/s], R1=R2=1 [Ω], L=0.1 [H], C=0.1 [F].
1) Draw the phasor diagram (vector diagram) of the relation between E, V1, V2, V3 and I.
2) Find the effective power (power consumption) of the entire circuit.

I got the answer for the second question, P=6000W.

 

[gneill]

Well, here's the actual question.
In the diagram’s circuit, the effective value of E is 100 [V], angular frequency is 10[rad/s], R1=R2=1 [Ω], L=0.1 [H], C=0.1 [F].
1) Draw the phasor diagram (vector diagram) of the relation between E, V1, V2, V3 and I.
2) Find the effective power (power consumption) of the entire circuit.

I got the answer for the second question, P=6000W.

So it looks like E should provide your reference phase (that is, it is assumed to have a phase of zero). I'd look at solving for the total impedance first, then find the total current I = E/Z. Then you can determine V1, V2, and V3 pretty easily. Do all this using complex values and you'll be able to extract the magnitudes and phases.

Your effective power value looks fine.

 

[MissP.25_5]

So it looks like E should provide your reference phase (that is, it is assumed to have a phase of zero). I'd look at solving for the total impedance first, then find the total current I = E/Z. Then you can determine V1, V2, and V3 pretty easily. Do all this using complex values and you'll be able to extract the magnitudes and phases.

Your effective power value looks fine.

Oh, I forgot something. In the question, it actually says to draw the phasor of the relation between all those vectors. So I assume that when it says "relation", we don't need to draw it very specifically, do we?

 

[gneill]

Oh, I forgot something. In the question, it actually says to draw the phasor of the relation between all those vectors. So I assume that when it says "relation", we don't need to draw it very specifically, do we?

Right, you don't need to choose a particular orientation. However, it's convenient to pick one of the phasors as a reference to work from . The supply voltage E looks to be convenient since its RMS magnitude is given, and in practice the source is generally the reference anyways.

 

[MissP.25_5]

Right, you don't need to choose a particular orientation. However, it's convenient to pick one of the phasors as a reference to work from . The supply voltage E looks to be convenient since its RMS magnitude is given, and in practice the source is generally the reference anyways.

So is my drawing wrong?

 

[gneill]

So is my drawing wrong?

I would reduce the angle between V3 and I. V2 and V3 are definitely not co-linear.

 

[MissP.25_5]

So it looks like E should provide your reference phase (that is, it is assumed to have a phase of zero). I'd look at solving for the total impedance first, then find the total current I = E/Z. Then you can determine V1, V2, and V3 pretty easily. Do all this using complex values and you'll be able to extract the magnitudes and phases.

Your effective power value looks fine.

Uhmm...how do you determine whether or not to take E as the reference?

 

[gneill]

Uhmm...how do you determine whether or not to take E as the reference?

As I stated previously (post #19), the power source for a circuit traditionally serves as the reference. It's not a rigid rule, so you may choose another current or voltage if you wish; it'll only alter the orientation of the diagram.

 

[MissP.25_5]

As I stated previously (post #19), the power source for a circuit traditionally serves as the reference. It's not a rigid rule, so you may choose another current or voltage if you wish; it'll only alter the orientation of the diagram.

Oh, I get it now. I fixed my drawing. Does this seem right?

 

[gneill]

Oh, I get it now. I fixed my drawing. Does this seem right?

Yes, that looks fine.

 

[MissP.25_5]

Yes, that looks fine.

THANK YOU SO MUCH!I posted a new thread, just to make sure I got it right. Can you take a look, please? After exam, I won't bother you as much anymore, haha.